Cómo determinar el tamaño mínimo necesario para una muestra estadística
El margen de error de un intervalo de confianza (IC) se ve afectada por las dimensiones de la muestra- estadística como el tamaño aumenta, margen de error disminuye. En cuanto a esta a la inversa, si quieres un menor margen de error (y no lo hace todo el mundo?), Se necesita una muestra de mayor tamaño.
Supongamos que usted está consiguiendo listo para hacer su propia encuesta para estimar una población significado ¿no sería agradable ver de antemano lo que muestra el tamaño que necesita para obtener el margen de error que quieres? Pensar en el futuro le ahorrará dinero y tiempo y que le dará los resultados que usted puede vivir con en términos de margen de error - no tendrá sorpresas más adelante.
La fórmula para el tamaño de muestra necesario para obtener un margen de error deseado (MOE) cuando usted está haciendo un intervalo de confianza para
siempre redondear el tamaño de la muestra no importa qué valor decimal que se obtiene. (Por ejemplo, si sus cálculos le dan 126,2 personas, puede no sólo tener 0.2 de una persona - que necesita toda la persona, por lo que incluirlo redondeando hasta 127.)
En esta fórmula, el Ministerio de Educación es el número que representa el margen de error que desee y, z* es el z*-valor correspondiente a su nivel de confianza deseado (de la continuación mesa- mayoría de las personas utilizan 1,96 para un intervalo de confianza del 95%).
| z*-valores para los distintos niveles de confianza | |
| Nivel de confianza | z * -valor |
|---|---|
| 80% | 1.28 |
| 90% | 1.645 (por convenio) |
| 95% | 1.96 |
| 98% | 2.33 |
| 99% | 2.58 |
Tenga en cuenta que estos valores se toman de la (Z) distribución estándar normal. La zona entre cada valor z * y el negativo de ese valor z * es el porcentaje de confianza (aproximadamente). Por ejemplo, el área entre z * = 1,28 y z = -1.28 es de aproximadamente 0,80. Por lo tanto esta tabla se puede ampliar a otros porcentajes de confianza también. El gráfico muestra sólo los porcentajes de confianza más comúnmente utilizados.
Si la desviación estándar de la población,
se desconoce, usted puede poner en un escenario suposición del peor caso para ello o ejecutar un estudio piloto (un estudio pequeño ensayo) antes de tiempo, encontrar la desviación estándar de los datos de la muestra (s), Y el uso de ese número. Esto puede ser riesgoso si el tamaño de la muestra es muy pequeña porque es menos probable que refleje toda la población- intento de conseguir el estudio ensayo más grande que se puede, y / o hacer una estimación conservadora de
A menudo, un estudio pequeño ensayo vale la pena el tiempo y esfuerzo. No sólo va a obtener una estimación de
para ayudar a determinar un buen tamaño de la muestra, pero también se puede aprender acerca de los posibles problemas en su recolección de datos.
He aquí un ejemplo en el que es necesario calcular n para estimar una media de la población. Suponga que desea estimar el número medio de canciones universidad tienda de los estudiantes en sus dispositivos portátiles. Usted quiere que el margen de error para ser no más de más o menos 20 canciones. ¿Quieres un intervalo de confianza del 95%. ¿Cuántos estudiantes en caso de que la muestra?
Porque quieres un IC del 95%, z * es 1,96 (que se encuentra en la tabla anterior) - usted sabe que su MOE deseado es 20. Ahora usted necesita un número de la desviación estándar de la población,
Este número no se conoce, por lo que hacer un estudio piloto de 35 alumnos y encontrar la desviación estándar (s) Para la muestra es de 148 canciones - utilizar este número como un sustituto de la
Utilizando la fórmula de tamaño de la muestra, se calcula el tamaño de la muestra que se necesita es
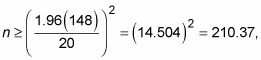
que redondear arriba a 211 alumnos (siempre se redondea hacia arriba en el cálculo n). Así que hay que tomar una muestra aleatoria de Al menos 211 estudiantes universitarios con el fin de tener un margen de error en el número de canciones almacenadas de no más de 20. Es por eso que se ve un mayor-que o-igual-a firmar en la fórmula aquí.
Siempre se redondea al número entero más próximo al calcular el tamaño de la muestra, sin importar el valor decimal del resultado es (por ejemplo, 0,37). Eso es porque desea que el margen de error para ser no más de lo que usted dijo. Si redondear hacia abajo cuando el valor decimal es menor de 0,50 (como lo hace normalmente en otros cálculos matemáticos), el Ministerio de Educación será un poco más grande de lo que quería.



