Cómo calcular el margen de error para una media muestral
Cuando una pregunta de investigación pide a encontrar una estadística media de la muestra (o promedio), es necesario reportar un margen de error, o el Ministerio de Educación, para la media de la muestra. La fórmula general para el margen de error de la media de la muestra (suponiendo una cierta condición se cumple - véase más adelante) se
es la desviación estándar de la población, n es el tamaño de la muestra, y z * es la apropiada z *-valor por su nivel deseado de confianza (que se puede encontrar en la siguiente tabla).
| z *-Los valores para seleccionadas (Porcentaje) ConfidenceLevels | |
| Porcentaje Confianza | z* -Valor |
|---|---|
| 80 | 1.28 |
| 90 | 1,645 |
| 95 | 1.96 |
| 98 | 2.33 |
| 99 | 2.58 |
Tenga en cuenta que estos valores se toman de la (Z) distribución estándar normal. La zona entre cada valor z * y el negativo de ese valor z * es el porcentaje de confianza (aproximadamente). Por ejemplo, el área entre z * = 1,28 y z = -1.28 es de aproximadamente 0,80. Esta tabla se puede ampliar a otros porcentajes de confianza también. El gráfico muestra sólo los porcentajes de confianza más comúnmente utilizados.
Estos son los pasos para calcular el margen de error para una media de la muestra:
Encuentra la desviación estándar de la población y el tamaño de la muestra, n.
La desviación estándar de la población,
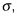
se dará en el problema.
Divida la desviación estándar de la población por la raíz cuadrada del tamaño de la muestra.
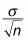
le da el error estándar.
Multiplique por el adecuado z *-valor (consulte la tabla anterior).
Por ejemplo, el z *-valor es de 1.96 si quieres estar cerca del 95% de confianza.
La condición que necesita para cumplir con el fin de utilizar un z *-valor en el margen de fórmula error para una media de la muestra es o bien: 1) La población original tiene una distribución normal, para empezar, o 2) El tamaño de la muestra es lo suficientemente grande para la distribución normal se puede utilizar (es decir, el límite central Teorema aplica). En general, el tamaño de la muestra, n, debe estar por encima de alrededor de 30 para que el teorema del límite central sea aplicable. Ahora, si es 29, no se preocupe - 30 no es un número mágico, que es sólo una regla general. (La desviación estándar de la población se debe conocer cualquier manera.)
He aquí un ejemplo: Supongamos que usted es el gerente de una tienda de helados, y ya está entrenando a los nuevos empleados sean capaces de llenar los conos de gran tamaño con la cantidad adecuada de helado (10 onzas cada uno). Usted quiere estimar el peso medio de los conos que hacen durante un período de un día, incluyendo un margen de error. En lugar de un peso cada cono único hecho, usted pide cada uno de sus nuevos empleados para detectar azar comprobar el peso de una muestra aleatoria de los grandes conos que hacen y registrar los pesos en una libreta. por n = 50 muestras de conos, la media de la muestra se encontró que era 10,3 oz. Supongamos que la desviación estándar de población es de 0,6 oz.
¿Cuál es el margen de error? (Supongamos que desea un nivel de 95% de confianza.) Se calcula así:
Así que reportar estos resultados, usted dice que en base a la muestra de 50 conos, a estimar que el peso promedio de todos los conos grandes hechas por los nuevos empleados durante un período de un día es de 10.3 onzas, con un margen de error de más o menos 0.17 oz. En otras palabras, el rango de valores probables para el peso medio de todos los grandes conos hechos para el día se estima (con 95% de confianza) para estar entre 10,30 - 0,17 = 10,13 oz y 10.30 + 0.17 = 10.47 oz. Los nuevos empleados parecen estar dando demasiada helado (aunque los clientes probablemente no son demasiado ofendido).
Observe en este ejemplo, las unidades son onzas, no porcentajes! Cuando se trabaja con y reportar los resultados acerca de los datos, recuerda siempre lo que las unidades son. Además, asegúrese de que las estadísticas se presentan con sus unidades de medida correctas, y si no lo son, preguntar lo que las unidades son.
En los casos donde n es demasiado pequeña (en general, menos de 30) para el teorema del límite central para ser utilizado, pero usted todavía piensa que los datos provienen de una distribución normal, se puede utilizar un t *-valor en lugar de una z* -valor en sus fórmulas. LA t *-valor es uno que proviene de una t-de distribución con n - 1 grados de libertad. De hecho, muchos estadísticos seguir adelante y utilización t *-valores en lugar de z *-valores constantemente, ya que si el tamaño de la muestra es grande, t *-valores y z *-los valores son aproximadamente iguales de todos modos. Además, para los casos en que no conoce la desviación estándar de la población,
se puede sustituir con s, la desviación-estándar de la muestra a partir de ahí se utiliza un t *-valor en lugar de una z *-valor en sus fórmulas también.




