Cómo determinar el intervalo de confianza para una proporción de la población
Usted puede encontrar el intervalo de confianza (IC) para una proporción de la población para mostrar la probabilidad estadística de que es probable que se produzcan dentro de la población de una característica.
Cuando una característica que se mide es categórica - por ejemplo, la opinión sobre un tema (de apoyo, se oponen o son neutrales), sexo, partido político, o el tipo de comportamiento (hacer / no usar el cinturón de seguridad durante la conducción) - la mayoría de la gente quiere para estimar la proporción (o porcentaje) de personas en la población que se encuentran en una determinada categoría de interés. Por ejemplo, considere el porcentaje de personas a favor de una semana de trabajo de cuatro días, el porcentaje de republicanos que votaron en la última elección, o la proporción de conductores que no usan el cinturón de seguridad. En cada uno de estos casos, el objeto es estimar una proporción de la población, p, utilizando una proporción de muestra,
más o menos un margen de error. El resultado se denomina una intervalo de confianza para la proporción poblacional, p.
La fórmula para un CI para una proporción de la población es
es la proporción de la muestra, n es el tamaño de la muestra, y z * es el valor apropiado de la distribución normal estándar para su nivel de confianza deseado. La siguiente tabla muestra los valores de z * para ciertos niveles de confianza.
| z*-valores para los distintos niveles de confianza | |
| Nivel de confianza | z * -valor |
|---|---|
| 80% | 1.28 |
| 90% | 1.645 (por convenio) |
| 95% | 1.96 |
| 98% | 2.33 |
| 99% | 2.58 |
Para calcular una CI de una proporción de la población:
Determinar el nivel de confianza y encontrar el adecuado z *-valor.
Consulte la tabla de arriba para z*-valores.
Encuentra la proporción de la muestra,
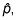
dividiendo el número de personas en la muestra que tiene la característica de interés por el tamaño de la muestra (n).
Nota: Este resultado debe ser un valor decimal entre 0 y 1.
Multiplicar
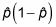
y luego dividir esa cantidad por n.
Toma la raíz cuadrada del resultado del paso 3.
Multiplica tu respuesta z *.
Este paso le da el margen de error.
Llevar
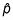
más o menos el margen de error para obtener el CI- el extremo inferior de la CI es
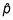
menos el margen de error, y el extremo superior de la CI es
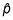
más el margen de error.
La fórmula que se muestra en el ejemplo anterior para un CI para p se utiliza bajo la condición de que el tamaño de la muestra es lo suficientemente grande para que el teorema del límite central a aplicar y permite utilizar un z*-valor, lo que ocurre en los casos cuando se está estimando proporciones basado en encuestas a gran escala. Para los pequeños tamaños de muestra, intervalos de confianza para la proporción son típicamente más allá del alcance de un curso de estadística de introducción.
Por ejemplo, suponga que desea calcular el porcentaje del tiempo (con una confianza del 95%) que se espera que obtener una luz roja en una cierta intersección. Supongamos que usted toma una muestra aleatoria de 100 viajes diferentes a través de esta intersección y usted encontrará que una luz roja fue golpeado 53 veces.
Porque quieres un intervalo de confianza del 95%, su z *-valor es 1,96.
La luz roja se golpeó 53 de cada 100 veces. Así
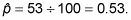
Encontrar
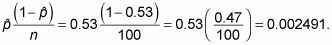
Tome la raíz cuadrada para obtener 0,0499.
El margen de error es, por lo tanto, más o menos 1,96 # 8727- 0,0499 = 0,0978, o 9,78%.
Su intervalo de confianza del 95% para el porcentaje de veces que tendrá que golpear una luz roja en esa intersección particular es 0.53 (o 53%), más o menos 0,0978 (redondeado a 0,10 o 10%). (El extremo inferior del intervalo es de 0,53 - 0,10 = 0,43 o 43% - el extremo superior es 0,53 + 0,10 = 0,63 o 63%).
Para interpretar estos resultados en el contexto del problema, se puede decir que con una confianza del 95% el porcentaje de las veces que se debe esperar para golpear una luz roja en esta intersección se sitúa entre 43% y 63%, basado en su muestra.




