Cómo estimar la diferencia entre dos proporciones
Para estimar la diferencia entre dos proporciones de población con un intervalo de confianza, puede utilizar el teorema del límite central, cuando los tamaños de las muestras son lo suficientemente grandes (por lo general, cada uno por lo menos 30). Cuando una característica estadística, tales como la opinión sobre un tema (apoyo / no soportan), de los dos grupos que se comparan es categórica, la gente quiere informar sobre las diferencias entre las dos proporciones de población - por ejemplo, la diferencia entre la proporción de hombres y mujeres que apoyan a una semana laboral de cuatro días. ¿Cómo haces esto?
Usted calcula la diferencia entre dos proporciones poblacionales, p1 - p2, tomando una muestra de cada población y el uso de la diferencia de las dos proporciones de muestra,
más o menos un margen de error. El resultado se denomina una intervalo de confianza para la diferencia de dos proporciones de la población, p1 - p2.
La fórmula para un intervalo de confianza (IC) para la diferencia entre dos proporciones poblacionales es
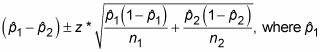
y n1 son del tamaño proporción de la muestra y de la muestra de la primera muestra, y
y n2 son la proporción de la muestra y tamaño de la muestra de la segunda muestra. El valor z * es el valor apropiado de la distribución normal estándar para su nivel de confianza deseado. (Consulte la tabla siguiente para z *-los valores.)
| z*-valores para los distintos niveles de confianza | |
| Nivel de confianza | z * -valor |
|---|---|
| 80% | 1.28 |
| 90% | 1.645 (por convenio) |
| 95% | 1.96 |
| 98% | 2.33 |
| 99% | 2.58 |
Para calcular un IC para la diferencia entre dos proporciones poblacionales, haga lo siguiente:
Determinar el nivel de confianza y encontrar el adecuado z *-valor.
Referirse a la tabla anterior.
Encuentra la proporción muestral
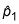
para la primera muestra, tomando el número total de la primera muestra de que están en la categoría de interés y dividiendo por el tamaño de la muestra, n1. Del mismo modo, encontrar
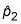
para la segunda muestra.
Tome la diferencia entre las proporciones de la muestra,
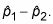
Encontrar
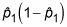
y dividir que por n1. Encontrar
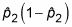
y dividir que por n2. Añadir estos dos resultados juntos y sacar la raíz cuadrada.
Multiplicar z * veces el resultado del paso 4.
Este paso le da el margen de error.
Llevar
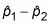
más o menos el margen de error de la Etapa 5 para obtener el CI.
El extremo inferior de la IC es
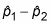
menos el margen de error, y el extremo superior de la CI es
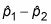
más el margen de error.
La fórmula que se muestra aquí un CI de p1 - p2 se utiliza bajo la condición de que ambos de los tamaños de las muestras son lo suficientemente grande para que el teorema del límite central a aplicar y le permiten utilizar un z* -value- esto es cierto cuando se está estimando proporciones utilizando encuestas a gran escala, por ejemplo. Para los pequeños tamaños de muestra, intervalos de confianza están más allá del alcance de un curso de estadística de introducción.
Suponga que usted trabaja para la Cámara de Las Vegas de Comercio, y desea estimar con una confianza del 95% de la diferencia entre el porcentaje de todas las mujeres que alguna vez han ido a ver a un imitador de Elvis y el porcentaje de todos los hombres que nunca han ido a ver a un imitador de Elvis, con el fin de ayudar a determinar cómo se debe comercializar sus ofertas de entretenimiento.
Porque quieres un intervalo de confianza del 95%, su z *-valor es 1,96.
Suponga que su muestra aleatoria de 100 mujeres incluye 53 mujeres que han visto un imitador de Elvis, así
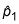
es 53 dividido por 100 = 0,53. Supongamos también que su muestra aleatoria de 110 hombres incluye 37 hombres que han visto nunca un imitador de Elvis, así
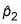
es 37 dividido por 110 = 0,34.
La diferencia entre estas proporciones muestrales (mujeres - hombres) es desde 0,53 hasta 0,34 = 0,19.
Tome 0.53 # 8727- (1 - 0,53) para obtener 0,2941. Luego divida que por 100 para obtener 0,0025. Luego tome 0.34 # 8727- (1 - 0.34) para obtener 0,2244. Luego divida que por 110 para obtener 0,0020. Añadir estos dos resultados para obtener 0.0025 + 0.0020 = 0.0045. A continuación, busque la raíz cuadrada de 0.0045 que es 0.0671.
1.96 # 8727- 0.0671 te da 0,13, o 13%, que es el margen de error.
Su intervalo de confianza del 95% para la diferencia entre el porcentaje de mujeres que han visto un imitador de Elvis y el porcentaje de hombres que han visto un imitador de Elvis es 0,19 o 19% (lo que tienes en el paso 3), más o menos el 13%. El extremo inferior del intervalo es de 0,19 - 0,13 = 0,06 o 6% - el extremo superior es 0,19 + 0,13 = 0,32 o 32%.
Para interpretar estos resultados en el contexto del problema, se puede decir con una confianza del 95% de que un mayor porcentaje de mujeres que hombres han visto un imitador de Elvis, y la diferencia en estos porcentajes es en algún lugar entre el 6% y el 32%, en función de su muestra.
La tentación es decir, " Bueno, conocí a una mayor proporción de mujeres ha sido testigo de un imitador de Elvis, ya que la proporción de la muestra fue de 0,53 y para los hombres que sólo era 0.34. ¿Por qué aún necesito un intervalo de confianza "? Todos esos dos números te dicen es algo acerca de esas 210 personas muestreadas. También es necesario tener en cuenta la variación utilizando el margen de error para poder decir algo acerca de toda la población de hombres y mujeres.
Por supuesto, hay algunos chicos por ahí que no admitiría que habían visto jamás un imitador de Elvis (aunque probablemente han fingieron ser uno haciendo karaoke en algún momento). Esto puede crear un poco de sesgo en los resultados.
Tenga en cuenta que usted puede obtener un valor negativo para
Por ejemplo, si usted hubiera cambiado los hombres y mujeres, se habría conseguido -0,19 para esta diferencia. Eso está bien, pero se puede evitar diferencias negativas en las proporciones de la muestra por tener el grupo con la proporción mayor de muestras sirven como el primer grupo (en este caso, las mujeres).
Sin embargo, aunque el grupo con la proporción de la muestra más grande sirve como el primer grupo, a veces usted todavía obtener valores negativos en el intervalo de confianza. Supongamos que en el ejemplo anterior que sólo 0,43 de las mujeres habían visto un imitador de Elvis. Por lo tanto, la diferencia en las proporciones es 0,09, y el extremo superior del intervalo de confianza es 0,09 + 0,13 = 0,22 mientras que el extremo inferior es 0,09 - 0,13 = -0,04. Esto significa que la verdadera diferencia es razonable en cualquier lugar del 22% a más mujeres a 4% más hombres. Es muy cerca de decir con seguridad.




