El teorema del límite central: lo que es lo suficientemente grande

categoría Educación y lenguas / Matemáticas / Estadísticas

En pocas palabras, el teorema del límite central dice que usted puede utilizar la distribución normal para describir el comportamiento de una media muestral incluso si los valores individuales que componen la media de la muestra no son normales sí mismos. Pero esto sólo es posible si el tamaño de la muestra es " lo suficientemente grande ". Muchos libros de texto de estadística que le dirían que n

tendría que ser al menos 30.

Pero ¿por qué es n = 30 el punto de referencia? Muchas variables en la naturaleza, las finanzas y otras aplicaciones tienen una distribución que está muy cerca de la curva normal. Por ejemplo, observando la t-tabla, vemos que los diversos valores de t comenzará a llegar muy cerca de los valores de z en el momento de llegar a unos 30 grados de libertad. Una razón para esto es que la t-distribuciones y los comparten dos características importantes normales de distribución: Ellos son simétricas, y son unimodal (que tiene un pico).

Si la distribución de sus valores de datos individuales está muy lejos de cualquiera de estas cualidades, es posible que necesite más de un tamaño de muestra de 30 a utilizar el teorema del límite central. Cuanto más lejos los datos es de ser simétrica y unimodal, más datos que usted necesita.

Simetría

Si usted sabe o sospecha que su distribución original no es simétrica respecto a la media, entonces es posible que tenga un tamaño de muestra que es significativamente mayor que 30 para obtener la posible muestra significa mirar normal (y por lo tanto utilizar el teorema del límite central).

Considere el siguiente derecho; histograma sesgada, que registra el número de mascotas por familia.

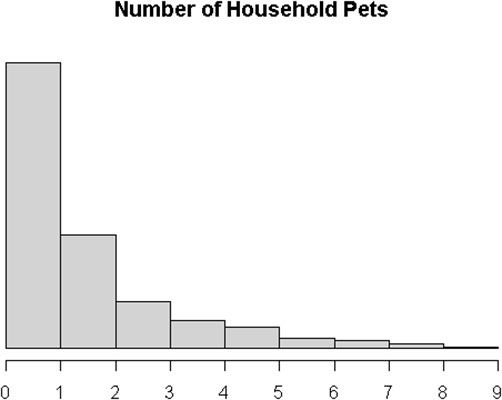
imagen0.jpg

Ahora, supongamos que representa a toda la población de los hogares. Usted repetidamente muestra n = 30 hogares de esa población. Esto es lo que la distribución de posibles medias muestrales se parece.

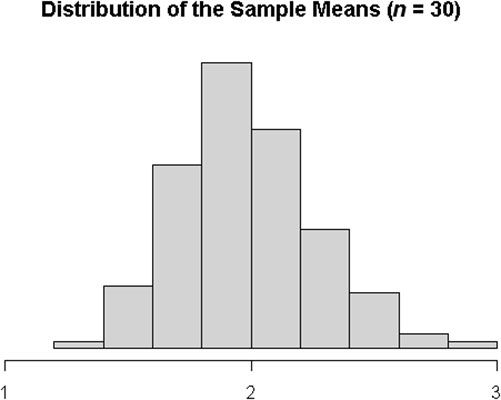
image1.jpg

Se puede ver que esta distribución no es normal porque la cola derecha todavía se extiende más lejos del pico central de la cola izquierda hace. No es simétrica. Para esta población, es necesario tomar una muestra de alrededor de n = 100 para obtener la muestra significa que conformarse en una curva simétrica.

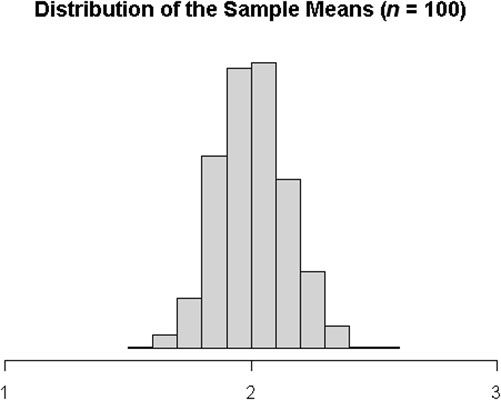
image2.jpg

Unimodal

Si usted sabe o sospecha que su distribución original no es unimodal y tiene más de un pico, entonces puede que tenga más de 30 en la muestra para sentirse bien sobre el uso del teorema del límite central.

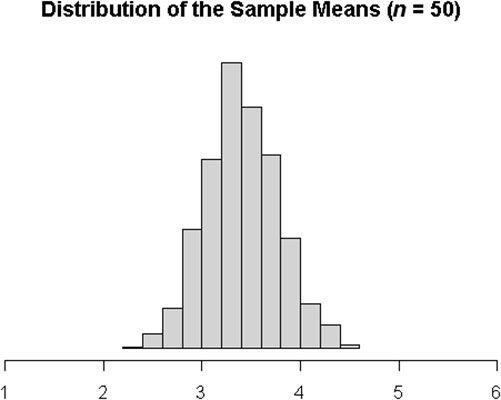
Considere el siguiente histograma población multimodal con tres picos distintos.

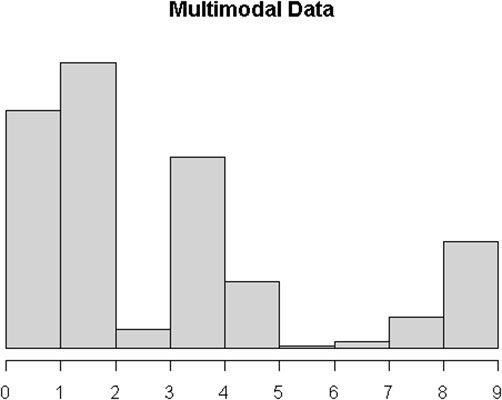
image3.jpg

Si sólo se muestra n = 30 de esa población, usted consigue una distribución unimodal, pero todavía no es del todo simétrica.

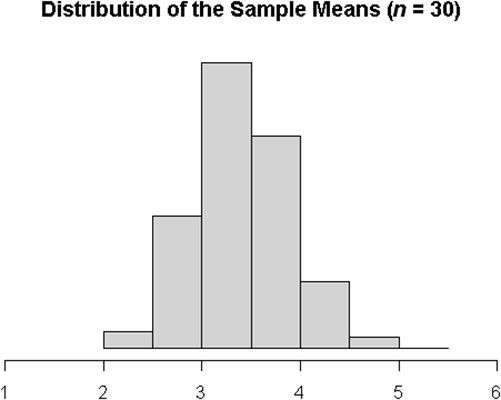
image4.jpg

Para esta población, lo que necesita para tomar una muestra de al menos n = 50 para estar seguro de que su media muestral distribución es más o menos normal.

image5.jpg

Artículos Relacionados

Sobre el autor
¿Cómo afecta el tamaño de la muestra error estándar ¿Cómo afecta el tamaño de la muestra error estándar

El tamaño (n) De una muestra estadística afecta el error estándar para esa muestra. Porque n se encuentra en el denominador de la fórmula error estándar, el error estándar disminuye a medida n aumenta. Tiene sentido que el tener más datos da…

¿Cómo se usa el teorema del límite central en las estadísticas ¿Cómo se usa el teorema del límite central en las estadísticas

La distribución normal se utiliza para ayudar a medir la exactitud de muchas estadísticas, incluida la media de la muestra, con un resultado importante llamado Teorema del límite central. Este teorema le da la capacidad de medir la cantidad de…

Cómo el número de grados de libertad afecta a la gráfica de una distribución t Cómo el número de grados de libertad afecta a la gráfica de una distribución t

Una de las propiedades interesantes de la distribución t es que cuanto mayor es el grado de libertad, más de cerca la distribución t se asemeja a la distribución normal estándar. A medida que los grados de libertad aumenta, el área en las…

Cómo calcular el margen de error para una media muestral Cómo calcular el margen de error para una media muestral

Cuando una pregunta de investigación pide a encontrar una estadística media de la muestra (o promedio), es necesario reportar un margen de error, o el Ministerio de Educación, para la media de la muestra. La fórmula general para el margen de…

Cómo convertir una distribución de muestreo a una variable aleatoria normal estándar usando el teorema del límite central Cómo convertir una distribución de muestreo a una variable aleatoria normal estándar usando el teorema del límite central

Puede utilizar el teorema del límite central para convertir una distribución muestral de una variable aleatoria normal estándar. Con base en el teorema del límite central, si dibuja muestras de una población que es mayor o igual a 30, entonces…

¿Cómo encontrar percentiles de una distribución t ¿Cómo encontrar percentiles de una distribución t

Cuando usted quiere encontrar percentiles para un t-distribución, se puede utilizar el t-mesa. LA percentil es un número en una distribución estadística cuya menos que la probabilidad es la porcentaje- dada por ejemplo, el percentil 95 de la…

¿Cómo encontrar probabilidades para una media muestral ¿Cómo encontrar probabilidades para una media muestral

En las estadísticas, usted puede encontrar fácilmente las probabilidades de una media muestral si tiene una distribución normal. Incluso si no tiene una distribución normal, o la distribución no se conoce, se puede encontrar probabilidades si…

¿Cómo encontrar la distribución de muestreo de una proporción de la muestra ¿Cómo encontrar la distribución de muestreo de una proporción de la muestra

Si utiliza un tamaño suficiente gran muestra estadística, se puede aplicar el teorema del límite central (CLT) a una proporción de la muestra para los datos categóricos para encontrar su distribución muestral. los proporción de la población,…

¿Cómo decirle a un z-distribución de una distribución t ¿Cómo decirle a un z-distribución de una distribución t

Aunque la normal (Z-) Distribución y t-distribución son similares, se ven diferentes entre sí y se utilizan para diferentes fines estadísticos. La distribución normal es que la distribución en forma de campana conocida cuya media esy cuya…

¿Cómo se utilizan los valores z en las estadísticas ¿Cómo se utilizan los valores z en las estadísticas

Si un conjunto de datos estadísticos tiene una distribución normal, se acostumbra a estandarizar todos los datos para obtener puntuaciones estándar conocido como z-valores o z-puntajes. La distribución de z-valores adquiere una distribución…

Distribuciones estadísticas: binomial, y t-distribución normal Distribuciones estadísticas: binomial, y t-distribución normal

Una distribución estadística es una lista de los posibles valores de una variable (o intervalos de valores) y la frecuencia (o en qué densidad) que se produzcan. Se puede tomar varias formas, incluyendo binomial, normal, y t-distribución.LA…

Distribuciones de probabilidad continuas Distribuciones de probabilidad continuas

Cuando se trabaja con distribuciones de probabilidad continuas, las funciones pueden tomar muchas formas. Estos incluyen uniforme continua, exponencial, normal, normal estándar (Z), la aproximación binomial, Poisson aproximación, y distribuciones…

» » » » El teorema del límite central: lo que es lo suficientemente grande