¿Cómo encontrar probabilidades para una proporción de la muestra
Usted puede encontrar las probabilidades de una proporción de la muestra mediante el uso de la aproximación normal, siempre y cuando se cumplan ciertas condiciones. Por ejemplo, digamos que un estudio estadístico afirma que 0,38 o 38% de todos los estudiantes que toman el examen ACT les gustaría ayuda y matemáticas. Supongamos que usted toma una muestra aleatoria de 100 estudiantes. ¿Cuál es la probabilidad de que más de 45 de ellos dicen que necesitan ayuda de matemáticas? En términos de proporciones, esto es equivalente a la probabilidad de que más de
Para responder a esta pregunta, primero compruebe las condiciones: En primer lugar, es np (tamaño de la muestra * población proporción) al menos 10? Sí, porque 100 # 8727- 0.38 = 38. A continuación, es n(1 - p) Al menos 10? Una vez más, sí, ya que el 100 # 8727- (1-0,38) = 62 cheques. Así que usted puede seguir adelante y utilizar la aproximación normal.
Usted hace la conversión de la
a una z-valorar el uso de la siguiente ecuación general:
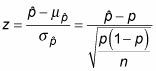
Cuando se conecta en los números para este ejemplo, se obtiene:
Es muy importante que preste atención a qué valor refleja la proporción de la población p y cuyo valor se calculó como la proporción de la muestra, p-sombrero. Flip-dejándose caer en la fórmula para z daría lugar a una respuesta muy diferente.
Y luego a encontrar P (Z > 1.44), utilizando la siguiente tabla.
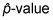
A partir de la tabla, se determina que P (Z > 1,44) = 1 - 0,9251 = 0,0749. Así que si es cierto que el 38 por ciento de todos los estudiantes que toman el examen quieren ayudar a las matemáticas, a continuación, en una muestra aleatoria de 100 estudiantes de la probabilidad de encontrar más de 45 que necesitan ayuda de matemáticas es aproximadamente 0,0749 (por el teorema del límite central).
Puede utilizar proporciones muestrales de revisar un reclamo sobre una parte de la población. (Este procedimiento es una prueba de hipótesis para una proporción de la población). En el ejemplo ACT, la probabilidad de que más del 45% de los estudiantes en una muestra de 100 necesitan ayuda matemáticas (cuando usted asumió el 38% de la población necesitaba ayuda matemáticas) fue encontrado que es 0,0749. Debido a que esta probabilidad es superior a 0,05 (el punto de corte típico para soplar el silbato en una reclamación sobre un valor de la población), no podrá disputar su afirmación de que el porcentaje de la población que necesita ayuda matemática es sólo el 38%. Este resultado muestra no es sólo un acontecimiento bastante raro.
-
Poniendo las variables en la misma escala: la distribución normal estándar (z) -
1.001 Estadísticas problemas de práctica para los maniquíes -
Los intervalos de confianza y las proporciones de población -
Sacar conclusiones sobre una población con intervalos de confianza y pruebas de hipótesis - Generalizando los resultados estadísticos a toda la población
-
Cómo comparar dos proporciones poblacionales
Cómo convertir una distribución de muestreo a una variable aleatoria normal estándar usando el teorema del límite central Puede utilizar el teorema del límite central para convertir una distribución muestral de una variable aleatoria normal estándar. Con base en el teorema del límite central, si dibuja muestras de una población que es mayor o igual a 30, entonces…
Cómo determinar un valor de p al probar una hipótesis nula Al probar una hipótesis sobre una población, puede utilizar el estadístico de prueba para decidir si se debe rechazar la hipótesis nula, H0. A tomar esta decisión mediante la presentación de un número, llamado p-valor.LA p-valor es una…
Cómo determinar el intervalo de confianza para una proporción de la población Usted puede encontrar el intervalo de confianza (IC) para una proporción de la población para mostrar la probabilidad estadística de que es probable que se produzcan dentro de la población de una característica.Cuando una característica que se…
Cómo estimar la diferencia entre dos proporciones Para estimar la diferencia entre dos proporciones de población con un intervalo de confianza, puede utilizar el teorema del límite central, cuando los tamaños de las muestras son lo suficientemente grandes (por lo general, cada uno por lo menos…
¿Cómo encontrar los momentos de la distribución binomial Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. El valor esperado representa el valor medio o promedio de una distribución. El valor esperado se conoce a…
¿Cómo encontrar la aproximación normal a la binomial con una amplia muestra n Si usted está trabajando de una gran muestra estadística, a continuación, la solución de problemas utilizando la distribución binomial puede parecer desalentador. Sin embargo, en realidad hay una manera muy fácil para aproximar la…
¿Cómo encontrar la distribución de muestreo de una proporción de la muestra Si utiliza un tamaño suficiente gran muestra estadística, se puede aplicar el teorema del límite central (CLT) a una proporción de la muestra para los datos categóricos para encontrar su distribución muestral. los proporción de la población,…
Cómo probar una hipótesis para la media de un población Usted puede utilizar una prueba de hipótesis para examinar o impugnar una reclamación estadística sobre una media poblacional si la variable es numérica (por ejemplo, edad, ingresos, tiempo, etc.) y sólo una población o grupo (como todos los…
Cómo probar una hipótesis nula basada en una proporción de la población Usted puede utilizar una prueba de hipótesis para probar un reclamo estadística sobre una proporción de la población cuando la variable es categórica (por ejemplo, el género o el apoyo / oposición) y está en estudio una sola población o…
Vinculación de margen de error y la población proporción Las preguntas de práctica aquí tienen que trabajar en el margen de error para los medios de la población y proporciones poblacionales. Resolver los siguientes problemas relacionados con el margen de error y la población proporción.La tabla…
Haciendo cálculos cuando se conocen las desviaciones estándar poblacionales Cuando nos fijamos en la diferencia entre dos medias (o dos proporciones), realizar un seguimiento de lo que las poblaciones que está llamando Población 1 y Población 2. Restar dos números en el orden opuesto cambia el signo de los…
Visión general de la prueba de hipótesis Una forma importante para sacar conclusiones acerca de las propiedades de una población es con la prueba de hipótesis. Puedes usar pruebas de hipótesis para comparar una medida de población a un valor especificado, comparar las medidas para dos…