Cómo probar una diferencia promedio utilizando la prueba t pareada
Puede probar una diferencia promedio utilizando el emparejado t-prueba cuando la variable es numérica (por ejemplo, los ingresos, el nivel de colesterol, o millas por galón) y los individuos de la muestra estadística están bien emparejado de alguna manera de acuerdo a las variables relevantes, como la edad o tal vez de peso, o las mismas personas son utilizado dos veces (por ejemplo, usando un pre-test y post-test).
Pruebas vinculados se utilizan normalmente para estudios en los que alguien está probando para ver si un nuevo tratamiento, la técnica o método funciona mejor que un método existente, sin tener que preocuparse de otros factores sobre los temas que pueden influir en los resultados.
Con la diferencia de la media, hacer coincidir los sujetos por lo que son considerados como provenientes de una sola población, y el conjunto de diferencias medidas para cada sujeto (por ejemplo, antes de la prueba frente a post-test) se considera como una muestra. La prueba de hipótesis y luego se reduce a una prueba para una media poblacional.
Por ejemplo, supongamos que un investigador quiere ver si los estudiantes de enseñanza para leer usando un juego de ordenador da mejores resultados que la enseñanza con un método fonética probada y verdadera. Ella selecciona al azar 20 estudiantes y las pone en 10 pares de acuerdo a su nivel de preparación para la lectura, la edad, el índice de inteligencia, y así sucesivamente. Ella selecciona al azar un estudiante de cada pareja a aprender a leer mediante el método de juego de ordenador (CM abreviado), y el otro en la pareja aprende a leer con el método fonético (PM abreviado). Al final del estudio, cada estudiante toma la misma prueba de lectura. Los datos se muestran en la siguiente tabla.
| Las puntuaciones de lectura de juego de ordenador Methodversus Método Phonics | |||
| Estudiante Par | Método ordenador | Método Phonics | Diferencia (CM - PM) |
|---|---|---|---|
| 1 | 85 | 80 | +5 |
| 2 | 80 | 80 | 0 |
| 3 | 95 | 88 | +7 |
| 4 | 87 | 90 | -3 |
| 5 | 78 | 72 | +6 |
| 6 | 82 | 79 | +3 |
| 7 | 57 | 50 | +7 |
| 8 | 69 | 73 | -4 |
| 9 | 73 | 78 | -5 |
| 10 | 99 | 95 | +4 |
Los datos originales están en pares, pero estás realmente interesado sólo en la diferencia en las puntuaciones de lectura (fonética menos puntuación de lectura informática lectura score) para cada par, no las propias calificaciones de lectura. Entonces el diferencias emparejadas (las diferencias en los pares de puntajes) son el nuevo conjunto de datos. Usted puede ver sus valores en la última columna de la tabla.
Mediante el examen de las diferencias en los pares de observaciones, que realmente sólo tienen un único conjunto de datos, y sólo tiene una prueba de hipótesis para una media poblacional. En este ejemplo específico, la hipótesis nula es que la media (de las diferencias emparejadas) es 0, y la hipótesis alternativa es que la media (de las diferencias emparejadas) es mayor que 0.
Si los dos métodos de lectura son los mismos, la media de las diferencias emparejadas debe estar cerca de 0. Si el método de ordenador es mejor, la media de las diferencias emparejadas debe ser significativamente más de 0-, es decir, la puntuación de la lectura ordenador sería mayor que los fonemas puntuación.
La notación para la hipótesis nula es
(Los d en el subíndice simplemente le recuerda que usted está trabajando con las diferencias pareadas.)
La fórmula para la prueba estadística de las diferencias emparejadas es

muestra, y tn-1 es un valor en el t-de distribución con nd - 1 grados de libertad.
Se utiliza un t-distribución aquí porque en la mayoría o por pares emparejados experimentos, el tamaño de la muestra es pequeño y / o la desviación estándar de la población
Se desconoce, por lo que se estima por sd.
Para el cálculo de la estadística de prueba para las diferencias pareadas, haga lo siguiente:
Para cada par de datos, tomar el primer valor en el par menos el segundo valor en el par de encontrar la diferencia emparejado.
Piense en las diferencias como su nuevo conjunto de datos.
Calcule la media,
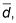
y la desviación estándar, sd, de todas las diferencias.
Dejando nd representar el número de diferencias pareadas que usted tiene, calcular el error estándar:
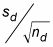
Dividir
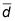
por el error estándar de la Etapa 3.
Porque
es igual a 0 si H0 Es cierto, que no necesita realmente para ser incluido en la fórmula de la estadística de prueba. Como resultado de ello, a veces se ve la estadística de prueba escrita de esta manera:
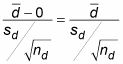
Para el ejemplo de las calificaciones de lectura, puede utilizar los pasos anteriores para ver si el método de la computadora es mejor en términos de enseñar a los estudiantes a leer.
Para encontrar la estadística, siga estos pasos:
Calcula las diferencias para cada par (que están mostrados en la columna 4 de la tabla anterior). Observe que la señal en cada una de las diferencias es importante- que indica que el método funcionó mejor para ese par particular.
Calcular la media y la desviación estándar de las diferencias desde el paso 1. En este ejemplo, la media de las diferencias es
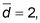
y la desviación estándar es de sd = 4.64. Tenga en cuenta que nd = 10 aquí.
El error estándar es
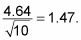
(Recuerde que aquí, nd es el número de pares, que es 10.)
Tomar la media de las diferencias (paso 2), dividido por el error estándar de 1,47 (Paso 3) para obtener 1,36, la estadística de prueba.
Es el resultado de la etapa 4 basta con decir que la diferencia en la lectura de las partituras encontradas en este experimento se aplica a toda la población en general? Debido a que la desviación estándar de población,
es desconocido y estimó que con la desviación estándar de la muestra (s), Es necesario utilizar el t-distribución en lugar de la Z-distribución a encontrar su p-valor. Usando el siguiente t-mesa, usted mira para arriba en el 1,36 t-distribución con 10 - 1 = 9 grados de libertad para calcular la p-valor.

los p-valor en este caso es mayor que 0,10 (y por lo tanto mayor que 0,05) debido a 1,36 es menor que (o a la izquierda de) el valor de 1,38 en la mesa, y por tanto su p-valor es superior a 0,10 (el p-valor para el título de la columna correspondiente a 1,38).
Porque el p-valor es mayor que 0.05, usted no puede rechazar H0- usted no tiene suficiente evidencia de que la diferencia media en las puntuaciones entre el método de la computadora y el método de la fonética es significativamente superior a 0. Sin embargo, eso no significa necesariamente una diferencia real no está presente en la población de todos los estudiantes. Pero el investigador no puede decir el juego de ordenador es un método de lectura mejor basado en esta muestra de 10 estudiantes.
Usted podría preguntarse, " Hey, la media muestral de las diferencias es de 2,0 lo que demuestra que el método de equipo era mejor que el método de la fonética. ¿Por qué la prueba de hipótesis rechazar H0 desde 2.0 es obviamente mayor que 0 "? Debido a que en este caso, 2,0 no es significativamente mayor que 0. También es necesario tener en cuenta la variación utilizando el error estándar y el t distribución de poder decir algo acerca de toda la población de estudiantes.




