Expresando funciona como serie de potencias utilizando la serie de Maclaurin
los Serie de Maclaurin es una plantilla que le permite expresar muchas otras funciones como series de potencias. Es la fuente de las fórmulas para expresar tanto el pecado X y cos X series como infinito.
Sin más preámbulos, aquí está:
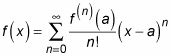
La notación F(n) medio " la nTH derivado de F." Esto se hace más claro en la versión ampliada de la serie de Maclaurin:
La serie de Maclaurin le permite expresar funciona como serie de potencias siguiendo estos pasos:
Encuentra las primeras derivadas de la función hasta que reconozcas un patrón.
Sustituto 0 para X en cada uno de estos derivados.
Conecte estos valores, término a término, en la fórmula para la serie de Maclaurin.
Si es posible, expresar la serie en notación sigma.
Por ejemplo, supongamos que usted quiere encontrar la serie de Maclaurin para eX.
Encuentra los primeros derivados de eX hasta que reconozcas un patrón:
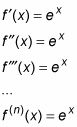
Sustituto 0 para X en cada uno de estos derivados.
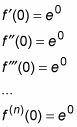
Conecte estos valores, término a término, en la fórmula para la serie de Maclaurin:
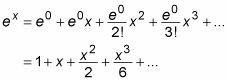
Si es posible, expresar la serie en notación sigma:
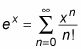
Para comprobar esta fórmula, lo utilizan para estimar e0 y e1 mediante la sustitución de 0 y 1, respectivamente, en los primeros seis términos:
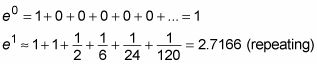
Este ejercicio uñas e0 exactamente, y se aproxima e1 con dos decimales. La serie de Maclaurin para eX Le permite calcular esta función para cualquier valor de X a cualquier número de cifras decimales.
Sin embargo, la serie de Maclaurin para eX funciona mejor cuando X está cerca de 0. Como X se aleja de 0, es necesario calcular más términos para obtener el mismo nivel de precisión.
Pero ahora, usted puede comenzar a ver por qué la serie de Maclaurin tiende a dar mejores aproximaciones a valores cercanos a 0: El número 0 es " cableado " en la fórmula como F(0), F'(0), F"(0), y así sucesivamente.
La figura ilustra este punto. El primer gráfico muestra el pecado X aproximada mediante el uso de los dos primeros términos de la serie de Maclaurin - que es, como el polinomio de tercer grado
El segundo gráfico muestra una aproximación del pecado X con cuatro términos.
Como puedes ver, cada aproximación sucesiva mejora sobre la anterior. Además, cada ecuación tiende a ofrecer su mejor aproximación cuando X está cerca de 0.
-
Los puertos serie en su PC -
Conexión de una serie con sus dos secuencias relacionadas -
La determinación de si una serie de Taylor es convergente o divergente -
Expresar y se aproximan a las funciones utilizando la serie de Taylor -
Expresando funciona como serie de potencias utilizando la serie de Taylor -
Expresando las cos función x como una serie
Expresando la función sen x como una serie Si usted quiere encontrar el valor aproximado del pecado X, puede utilizar una fórmula para expresarlo como una serie. Esta fórmula expresa la función seno como una serie alternante:Para darle sentido a esta fórmula, utilice la notación…
Cómo analizar una serie telescópica Usted no ve muchas series telescópica, pero la regla serie telescópica es buena para mantener en su bolsa de trucos - nunca se sabe cuando puede ser útil. Considere las siguientes series:Para ver que ésta es una serie telescópica, usted tiene…
Cómo analizar la convergencia absoluta y condicional Muchas series divergentes de términos positivos convergen si cambia las señales de sus condiciones de forma que alternan entre positivo y negativo. Por ejemplo, usted sabe que la serie armónica diverge:Pero, si cambia cualquier otro signo a…
Cómo analizar una serie p El llamado p-series son series relativamente simple, pero importante, que se puede utilizar como puntos de referencia para determinar la convergencia o divergencia de la serie más complicada. LA p-serie es de la forma(dónde p es un positivo…
Cómo determinar si una serie alternante converge o diverge Un alterno serie es una serie donde los términos alternan entre positivo y negativo. Se puede decir que una serie alternante converge si se cumplen dos condiciones:Su nº término converge a cero.Sus términos son no aumentando - en otras palabras,…
¿Cómo encontrar el valor de una suma infinita en una secuencia geométrica Si tu profesor de pre-cálculo le pide que encontrar el valor de una suma infinita en una secuencia geométrica, el proceso es muy simple - siempre y cuando usted mantenga sus fracciones y decimales recta. Si r se encuentra fuera del rango -1 lt; r…
¿Cómo integrar una serie de potencias Debido a la serie de potencia se asemejan polinomios, son fáciles de integrar el uso de un proceso de tres pasos simples que utiliza la regla de la suma, la Regla múltiplo constante, y la Regla de energía.Por ejemplo, echar un vistazo a la…
¿Cómo reconocer una serie p Un tipo importante de serie se llama la p-serie. LA p-serie puede ser divergente o convergente, en función de su valor. Se toma la siguiente forma:He aquí un ejemplo común de un p-serie, cuando p = 2:Aquí hay algunos otros ejemplos de…
Cómo utilizar la notación de sumatoria para mostrar una suma parcial de una secuencia Notación de sumatoria es una forma útil para representar la suma parcial de una secuencia. La suma de la primera k términos de una progresión aritmética se conoce como la ksuma parcial TH. Se llaman sumas parciales porque sólo eres capaz de…
Cómo utilizar la prueba de comparación límite para determinar si una serie converge La idea detrás de la prueba de comparación de límite es que si usted toma una serie convergente conocido y se multiplica cada uno de sus términos por algún número, luego que la nueva serie también converge. Y no importa si el multiplicador…
Cómo utilizar la prueba enésimo plazo para determinar si una serie converge Si los términos individuales de una serie (en otras palabras, los términos de secuencia subyacente de la serie) no convergen a cero, entonces la serie debe divergir. Este es el nprueba ª plazo para la divergencia. Esto es por lo general una muy…
¿Cómo trabajar con series geométricas Series geométricas son series relativamente simple, pero importante, que se puede utilizar como puntos de referencia para determinar la convergencia o divergencia de la serie más complicada. Una serie geométrica es una serie de la forma:El primer…