Cómo hacer aproximaciones lineales
Debido a que las funciones ordinarias son localmente lineal (que significa recto) - y cuanto más te acercas a ellos, el más recto que buscar-una línea tangente a una función es una buena aproximación de la función cerca del punto de tangencia.
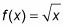
Esta figura muestra la gráfica de
y una línea tangente a la función en el punto (9, 3). Se puede ver que cerca (9, 3), la curva y la recta tangente son prácticamente indistinguibles.
La determinación de la ecuación de esta recta tangente es una brisa. Tienes un punto, (9, 3), y la pendiente está dada por la derivada de F a las 9:
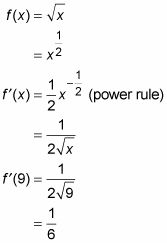
Ahora acaba de tomar esta pendiente, sexto, y el punto (9, 3), y conectarlos a la forma punto-pendiente:
Zoom en el punto (9, 3) un par de veces, y se ve que la curva se pone más recto y más recta y la línea curva y la tangente obtener más y más cerca.
Ahora, dice que quiere aproximar la raíz cuadrada de 10. Debido a que 10 es bastante cerca de 9, y porque se puede ver en la figura que F(X) Y su línea tangente están cerca entre sí en X = 10, el y-coordenadas de la línea en X = 10 es una buena aproximación del valor de la función en X = 10, a saber,
Sólo tiene que conectar 10 en la ecuación de la línea para su aproximación:
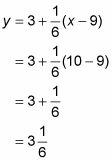
Por lo tanto, la raíz cuadrada de 10 es de aproximadamente
Esto es sólo el 0.004 más que la respuesta exacta de 3.1623 # 133-.El error es aproximadamente una décima parte de un por ciento.
Esta forma hace que sea más fácil hacer el cálculo y la más fácil de entender lo que está pasando cuando se computa una aproximación lineal. He aquí por qué. Usted sabe que la recta tangente pasa por el punto (9, 3), a la derecha? Y usted sabe la pendiente de la recta es 1/6. Por lo tanto, usted puede comenzar en (9, 3) y vaya a la derecha (o izquierda) a lo largo de la línea de la forma escalonada, como se muestra en la siguiente figura: más de 1, hasta 1 / 6- más de 1, hasta 1 / 6, y así sucesivamente.
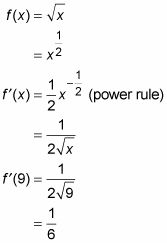
Así que, cuando estás haciendo una aproximación, se inicia en una y-valor de 3 y subir 6.1 por cada 1 que vaya a la derecha. O si usted va a la izquierda, hay que bajar 1/6 por cada 1 de ir a la izquierda. Cuando la ecuación línea está escrito en el formulario anterior, el cálculo de una aproximación lineal paralelo a este esquema escalonado.
La figura muestra los valores aproximados para las raíces cuadradas de 7, 8, 10, 11 y 12. Así es como te ocurrió con estos valores.
-
Dibuja círculos y tangentes en una TI-83 Plus gráfico -
Añadir una línea tangente a un gráfico en TI-Nspire -
Calcular la pendiente de una función utilizando el cociente de diferencias -
Cómo aproximar área con la regla trapezoidal -
Cómo determinar el costo marginal, el ingreso marginal y el beneficio marginal en la economía -
¿Cómo encontrar una línea normal a una curva
¿Cómo encontrar una línea normal perpendicular a una recta tangente Una línea normal a una curva en un punto dado es la línea perpendicular a la línea que es tangente en ese mismo punto. Encontrar los puntos de perpendicularidad para todas las líneas normales a la parábolaque pasan por el punto (3,…
¿Cómo encontrar la ecuación de asíntotas En pre-cálculo, puede que tenga que encontrar la ecuación de asíntotas para ayudarle a esbozar las curvas de una hipérbola. Debido a hipérbolas están formados por una curva donde la diferencia de las distancias entre dos puntos es constante,…
¿Cómo encontrar las líneas tangentes de una parábola que pasan por un punto determinado ¿Alguna vez quiso determinar la ubicación de una línea a través de un punto dado que es tangente a una curva dada? Por supuesto que tienes! He aquí cómo lo haces.Determinar los puntos de tangencia de las líneas por el punto (1, -1) que son…
Cómo graficar seno, coseno y tangente Así, es necesario graficar un seno, coseno, tangente o función. Seno, coseno y tangente - y sus inversos, cosecante, secante y cotangente - son periódico funciones, lo que significa que sus gráficos contienen una forma básica que se repite una…
¿Cómo saber cuando un derivado no existe Hay tres situaciones en las que un derivado de falla de existir. La derivada de una función en un punto dado es la pendiente de la recta tangente en ese punto. Por lo tanto, si no se puede trazar una línea tangente, no hay derivada - que sucede en…
¿Cómo trabajar con líneas en el cálculo Una línea es la función más simple que se puede representar gráficamente en el plano de coordenadas. (Líneas son importantes en el cálculo porque cuando te acercas lo suficiente en una curva, se ve y se comporta como una línea.) Esta figura…
El cociente de diferencias: el puente entre el álgebra (pendiente) y el cálculo (la derivada) Una de las piedras angulares de cálculo es el cociente de diferencias. El cociente de diferencias - junto con los límites - le permite tomar la fórmula pendiente edad ordinaria que utilizó para calcular la pendiente de las líneas en la clase de…
Cómo una tangente se refiere a un círculo Una línea es tangente a un círculo si toca al uno y sólo un punto. Si una línea es tangente a un círculo, entonces es perpendicular al radio trazado hasta el punto de tangencia. Echa un vistazo a las ruedas de la bicicleta en la siguiente…
Cómo determinar la medida de un ángulo cuyo vértice se encuentra fuera de un círculo Un ángulo que cruza un círculo puede tener su vértice en el interior, sobre o fuera del círculo. Este artículo aborda los tres tipos de ángulos que tienen sus vértices fuera de un círculo: ángulos secante-secantes, ángulos…
Acordes frente tangentes de los círculos Usted muestra el diámetro y el radio de un círculo dibujando segmentos a partir de un punto en el círculo, ya sea hacia oa través del centro del círculo. Sin embargo, otras dos figuras rectas tienen un lugar en un círculo. Una de estas figuras…
Funciones Gráfico tangente inversa y cotangente Las gráficas de las funciones tangente y cotangente son muy interesantes porque implican dos asíntotas horizontales. Las asíntotas ayudan con las formas de las curvas y hacer hincapié en el hecho de que algunos ángulos no funcionarán con las…
Múltiplos gráfica de la función tangente En trigonometría, valores tangentes van desde menos infinito hasta el infinito positivo. Así que cuando usted multiplica toda la función tangente de un número, esto es lo que sucede: Si se multiplica por un número mayor que 1, la función se…