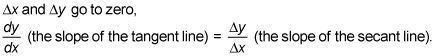Calcular la pendiente de una función utilizando el cociente de diferencias

Usted puede calcular la pendiente de una función mediante el cociente de diferencias. El cociente de diferencias le permite calcular una pendiente si no inicialmente tiene dos puntos de enchufe en la fórmula de la pendiente.

Para calcular una pendiente, necesita dos puntos para conectar a esta fórmula. Para una línea, esto es fácil. Usted acaba de recoger dos puntos cualesquiera de la línea y conectarlos. Pero no es tan simple, si usted quiere, por ejemplo, la pendiente de la parábola F (X) = X² en el punto (2, 4). Echa un vistazo a la primera figura.

Se puede ver la línea trazada tangente a la curva en (2, 4). Debido a la pendiente de la recta tangente es la misma que la pendiente de la parábola en (2, 4), todo lo que necesita es la pendiente de la recta tangente a darle la pendiente de la parábola. Pero usted no sabe la ecuación de la recta tangente, por lo que usted no puede conseguir el segundo punto -, además de (2, 4) - que usted necesita para la fórmula de la pendiente.

Así es como los inventores del cálculo llegaron alrededor de este obstáculo. La siguiente figura muestra la tangente de nuevo y una línea secante que corta la parábola en (2, 4) y al (10, 100).

Definicion de secante: Una línea secante es una línea que se cruza con una curva en dos puntos. Esto es un poco simplista, pero servirá.

La pendiente de esta recta secante está dada por la fórmula de la pendiente:

Se puede ver que esta línea secante es más pronunciada que la línea tangente, y por lo tanto la pendiente de la secante, 12, es mayor que la pendiente que estás buscando.

Ahora añade un punto más al (6, 36) y sacar otra secante utilizando ese punto y (2, 4) de nuevo, como se muestra en la siguiente figura.

Calcular la pendiente de esta segunda secante:

Se puede ver que esta línea secante es una mejor aproximación de la recta tangente a la primera secante.

Ahora, imagine lo que pasaría si agarraste el punto en (6, 36) y se deslizó hacia abajo la parábola hacia (2, 4), arrastrando la línea secante junto con él. ¿Puedes ver que a medida que el punto se acerca más y más cerca de (2, 4), la línea secante se acerca más y más cerca de la línea tangente, y que la pendiente de esta secante tanto, se acerca cada vez más cerca de la pendiente de la tangente?

Así, se puede obtener la pendiente de la tangente si se toma el límite de las pistas de este secante en movimiento. Vamos a darle el punto móvil las coordenadas (X₂, y₂). Como este punto (X₂, y₂) Se desliza cada vez más cerca (X₁, y₁), A saber (2, 4), el carrera, que es igual X₁ - X₁, se acerca más y más cerca de cero. Así que aquí está el límite de lo necesario:

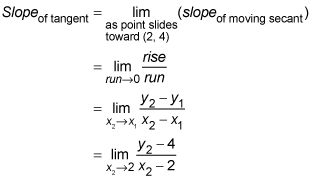
Mira lo que le pasa a este límite al conectar cuatro puntos más en la parábola que están más cerca y más cerca de (2, 4):

Cuando el punto (X₂, y₂) Se desliza a (3, 9), la pendiente es

o 5.Cuando el punto se desliza a (2.1, 4.41), la pendiente es

o 4.1.Cuando el punto se desliza a (2.01, 4.0401), la pendiente es 4,01.Cuando el punto se desliza a (2.001, 4.004001), la pendiente es 4.001.

Parece seguro como la pendiente se dirigían a 4.

Al igual que con todos los problemas de límite, la variable en este problema, X₂ enfoques pero en realidad nunca llega al número flecha (2 en este caso). Si llegó a 2 - lo que pasaría si se deslizó el punto que agarró a lo largo de la parábola hasta que era en realidad en la parte superior de (2, 4) - se obtendría

que es indefinido. Pero, por supuesto, la pendiente en (2, 4) es precisamente la pendiente desea - la pendiente de la línea cuando el punto hace tierra en la parte superior de (2, 4). En esto radica la belleza del proceso de límite. Con este límite, se obtiene la exacto pendiente de la tangente línea en (2, 4) a pesar de que la función de límite,

genera laderas de secante líneas.

Aquí de nuevo es la ecuación de la pendiente de la línea tangente:

Y la pendiente de la recta tangente es - usted lo adivinó - la derivada.

Significado del derivado de: La derivada de una función F(X) En algún número X = c, escrita como

es la pendiente de la recta tangente a F dibujado en c.

La fracción pendiente

se expresa con la terminología de álgebra. Ahora puede volver a escribir para darle ese aspecto cálculo highfalutin. Pero en primer lugar, por último, la definición que has estado esperando.

Definición de la cociente de diferencias: Hay un término elegante para el cálculo de la fracción pendiente general,

cuando se escribe en la forma de cálculo de fantasía. Una fracción es una cociente, ¿derecho? Y ambos y₂ - y₁ y X₂ - X₁ son diferencias, ¿derecho? Así, voil # 224-, se llama la cociente de diferencias. Aquí está:

(Esta es la forma más común de escribir el cociente de diferencias. Usted puede correr a través de otras formas, equivalentes.)

Bueno, vamos a diseñar este proceso en el que

se transforma en el cociente de diferencias.

En primer lugar, la carrera, X₂ - X₁ (en este ejemplo, X₂ - 2), se llama h. A continuación, porque X₁ = 2 y el carrera es igual a h, X₂ es igual a 2 + h. A continuación, escriba y₁ como F(2) y y₂ como F(2 + h). Hacer todas las sustituciones le da la derivada de X² a X = 2:

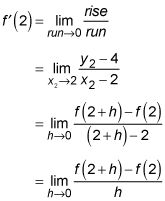
Recuerda que

es simplemente el encogimiento

paso de la escalera se puede ver en la f anteriorigura como el punto se desliza por la parábola hacia (2, 4).

La siguiente figura es básicamente el mismo que el anterior, excepto que en lugar de puntos exactos como (6, 36) y (10, 100), el punto de deslizamiento tiene las coordenadas generales de (2 + h, F (2 + h)), y el subir y el carrera se expresan en términos de h.

Así que esta cifra es la gráfica definitiva para

¿Está usted confundido por estas dos figuras? No te preocupes. Ambos muestran la misma cosa. Ambas figuras son representaciones visuales de

Hacer las matemáticas le da, al fin, la pendiente de la recta tangente en (2, 4):

Así que la pendiente en el punto (2, 4) es 4.

Definición principal de la derivado: Si reemplaza el punto (2, F(2)) en la ecuación de límite con el punto general (X, F (X)), Se obtiene la definición general de la derivada como una función de X:

Así que por fin se ve que el derivado se define como el límite del cociente de diferencias.

La siguiente figura muestra esta definición general gráficamente. Tenga en cuenta que esta cifra es prácticamente idéntica a la anterior, excepto que Xs reemplazar los 2s en la figura anterior y que el punto en movimiento en esta figura se desliza hacia abajo, hacia cualquier punto de edad (X, F (X)) En lugar de hacia el punto específico (2, F(2)).

Ahora averiguar este límite y obtener la derivada de la parábola, F(X) = X²:

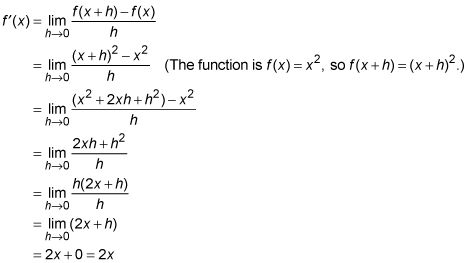
Así, por esta parábola, el derivado (que es la pendiente de la línea tangente en cada valor X) Es igual a 2X. Conecte cualquier número en X, y se obtiene la pendiente de la parábola en que X-valor. Intentalo.

La cifra final del tipo resume (en forma simplificada) todas las ideas precedentes difíciles sobre el cociente de diferencias.

Al igual que las tres figuras anteriores, la cifra final contiene un escalón básica pendiente, una línea secante y una tangente. La pendiente de la recta secante es

La pendiente de la recta tangente es

y se puede ver por qué es uno de los símbolos que se utilizan para la derivada. A medida que la línea secante de escalera se reduce a nada, o, en otras palabras, en el límite cuando