¿Cómo encontrar una línea normal perpendicular a una recta tangente

Una línea normal a una curva en un punto dado es la línea perpendicular a la línea que es tangente en ese mismo punto. Encontrar los puntos de perpendicularidad para todas las líneas normales a la parábola

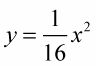
que pasan por el punto (3, 15):

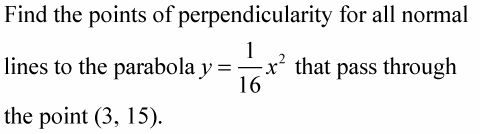
Representa gráficamente la parábola y trazar el punto (3, 15). Ahora, antes de que se hacen las cuentas, trata de aproximar las ubicaciones de todas las líneas normales. ¿Cuántos puede usted ver? Es bastante fácil ver que, a partir de (3, 15), una línea normal desciende ligeramente a la derecha y otro va un poco más inclinada hacia la izquierda. Pero ¿sabía usted encuentra el tercero que hay entre estos dos? No se preocupe si usted no vio este, porque cuando se hacen las cuentas, usted consigue las tres soluciones.

Al hacer el cálculo, o cualquier matemáticas para el caso, llegar a un sentido común, estimación aproximada de la solución a un problema antes de hacer los cálculos (cuando sea posible y el tiempo lo permite). Esto profundiza su comprensión de los conceptos involucrados y proporciona un cheque a la solución matemática.

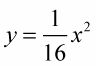
La figura muestra la parábola y las tres líneas normales.

En cuanto a la figura, se puede apreciar cómo la práctica de este problema. Va muy útil si quieres pasar a encontrarse de pie dentro de la curva de una pared parabólica, y desea saber la ubicación exacta de los tres puntos en la pared donde se puede lanzar una pelota y tener rebotar directamente a tú.

La solución es muy similar a la solución del problema de la tangente, excepto que en este problema se utiliza la regla para las líneas perpendiculares:

Las pendientes de rectas perpendiculares son recíprocos opuestos.

Cada línea normal en la figura es perpendicular a la línea tangente trazada en el punto donde la normal de la curva cumple. Así que la pendiente de cada línea normal es el recíproco opuesto de la pendiente de la tangente correspondiente - que, por supuesto, está dada por la derivada. Así que aquí va.

1. Tome un punto general (x, y), En la parábola

   

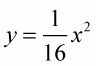
   y sustituto

   

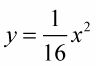
   para y.

   

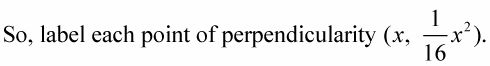
2. Tome la derivada de la parábola.

   

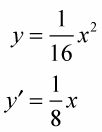
3. Utilizando la fórmula de la pendiente, ajuste la pendiente de cada línea normal a partir de (3, 15) a

   

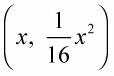
   igual al recíproco opuesto de la derivada en

   

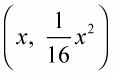
   y resolver para x.

   

   Ahora, no hay forma automática para obtener soluciones exactas a este cúbico (tercero grado) ecuación como la forma en la fórmula cuadrática te da la solución a una ecuación de segundo grado. En su lugar, se puede graficar

   

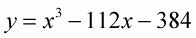
y el X-intercepta darle las soluciones, pero con este método, no hay garantía de que obtendrá soluciones exactas. (A menudo, las soluciones aproximadas son de lo mejor que puedes hacer con las ecuaciones cúbicas.) Aquí, sin embargo, que la suerte a cabo - en realidad yo tenía algo que ver con eso - y obtener las soluciones exactas de -8, -4 y 12.

1. Conecte cada uno de los X-coordenadas (-8, -4, y 12) en

   

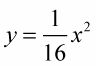
2. para obtener el y-coordenadas.

   

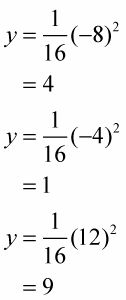
Por lo tanto, los tres puntos de normalidad son (-8, 4), (-4, 1), y (12, 9).