El cociente de diferencias: el puente entre el álgebra (pendiente) y el cálculo (la derivada)

Una de las piedras angulares de cálculo es el cociente de diferencias. El cociente de diferencias - junto con los límites - le permite tomar la fórmula pendiente edad ordinaria que utilizó para calcular la pendiente de las líneas en la clase de álgebra y utilizarla para la tarea de cálculo para calcular la pendiente (o derivado) de una curva. Así es como funciona.

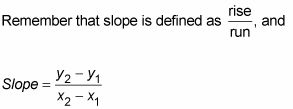
En el siguiente ejemplo, usted quiere encontrar la pendiente en un punto de la parábola.

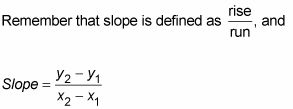
Para calcular la pendiente, necesita dos puntos para conectar a esta fórmula. Para una línea, esto es fácil. Usted acaba de recoger dos puntos cualesquiera de la línea y enchufar en.

Se puede ver la línea trazada tangente a la curva en (2, 4), y debido a la pendiente de la recta tangente es la misma que la pendiente de la parábola en (2, 4), todo lo que necesita es la pendiente de la tangente la línea. Pero usted no sabe la ecuación de la recta tangente, por lo que usted no puede conseguir el segundo punto -, además de (2, 4) - que usted necesita para la fórmula de la pendiente.

Así es como los inventores del cálculo llegaron alrededor de este obstáculo.

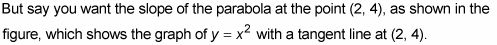
La figura de arriba es la gráfica de y = X² con una línea tangente y una secante. Se muestra la línea tangente de nuevo y una línea secante que intersecta la parábola en (2, 4) y al (10, 100).

LA secante es una línea que se cruza con una curva en dos puntos. Esto es un poco simplista, pero servirá.

La pendiente de esta recta secante está dada por la fórmula de la pendiente:

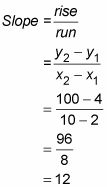
Se puede ver que esta línea secante es un poco más pronunciada que la línea tangente, y por lo tanto la pendiente de la secante, 12, es mayor que la pendiente que estás buscando.

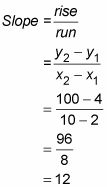
Ahora añade un punto más al (6, 36) y sacar otra secante utilizando ese punto y (2, 4) de nuevo. Ver la figura anterior.

Calcular la pendiente de esta segunda secante:

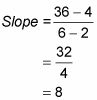
Se puede ver que la pendiente de esta recta secante es una mejor aproximación de la pendiente de la recta tangente a la pendiente de la primera secante era.

Ahora, imagine lo que pasaría si agarraste el punto en (6, 36) y se deslizó hacia abajo la parábola hacia (2, 4), arrastrando la línea secante junto con él. ¿Puedes ver que a medida que el punto se acerca más y más cerca de (2, 4), la línea secante se acerca más y más cerca de la línea tangente, y que la pendiente de esta secante tanto, se acerca cada vez más cerca de la pendiente de la tangente?

Así, se puede obtener la pendiente de la tangente si se toma el límite de la pendiente de la secante este movimiento.

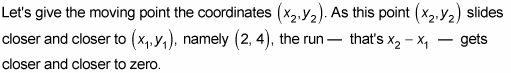
Así que aquí está el límite de lo necesario:

Mira lo que le pasa a este límite al conectar tres puntos más en la parábola que están más cerca y más cerca de (2, 4):

Cuando el punto se desliza a (2.01, 4.0401), la pendiente es 4,01

Cuando el punto se desliza a (2.001, 4.004001), la pendiente es 4.001

Parece seguro como la pendiente se dirigían a 4.

Al igual que con todos los problemas de límite, la variable en este problema, el carrera, enfoques pero en realidad nunca llega a cero. Si se puso a cero - que pasaría si se deslizó el punto que agarró a lo largo de la parábola hasta que era en realidad en la parte superior de (2, 4) - que tendría una pendiente de 0/0, que no está definido. Pero, por supuesto, eso es, precisamente, la pendiente que quieras - la pendiente de la línea cuando el punto hace tierra en la parte superior de (2, 4). En esto radica la belleza del proceso de límite.

Y la pendiente de la recta tangente es - usted lo adivinó - la derivada.

los derivado de una función, F(X), En algún número X = c, escrita como f '(c), Es la pendiente de la recta tangente a F dibujado en c.

Bueno, aquí está la forma más común de escribir el cociente de diferencias (puede correr a través de otras vías, equivalentes).

Echa un vistazo a la siguiente figura, que muestra cómo un límite produce la pendiente de la recta tangente en (2, 4).

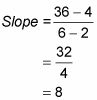
Hacer las matemáticas le da, al fin, la pendiente de la recta tangente en (2, 4):

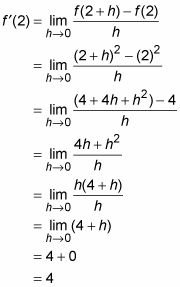
Así que la pendiente es 4. (Por cierto, que es una coincidencia sin sentido que la pendiente en (2, 4) pasa a ser la misma que la y-de coordenadas del punto).