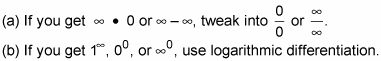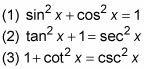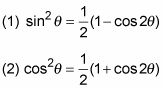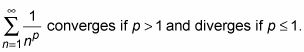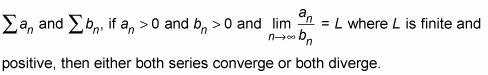La matemática de los límites de la base de todo del cálculo. Límites especie de permiten hacer zoom en la gráfica de una curva - más y más - hasta que se convierte en recta. Una vez que es recta, se puede analizar la curva con regularidad de edad, álgebra y geometría. Esa es la magia de cálculo en una pequeña cáscara de nuez.
Aquí hay algunas cosas importantes a tener en cuenta en la evaluación de los límites:
El límite en un agujero es la altura del agujero.
El límite en el infinito es la altura de la asíntota horizontal.
Antes de intentar otras técnicas, enchufe el número de flecha. Si el resultado es:
Un número, ya está.
Un número por encima de cero o infinito sobre cero, la respuesta es infinito.
Una serie sobre el infinito, la respuesta es cero.
0/0 o # 8734 - / # 8734-, utilice L'H # 244-pital Regla de.
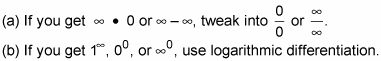
Cálculo: Cómo Resolver Problemas Diferenciación
En cálculo, la forma de resolver un problema derivado depende de qué forma el problema toma. Tipos de problemas comunes incluyen la cadena REGLA posición Optimization, la velocidad y las tasas acceleration- y relacionados. Aquí están algunas cosas a tener en cuenta al resolver cada tipo de problema:
Problemas de regla de la cadena
Use la regla de la cadena cuando el argumento de la función que estés diferenciador es más que un simple y llano X.
Trabajo de afuera, en.
No toque las cosas dentro.
Hacer sólo un derivado por paso.
Problemas de optimización
Exprese lo que usted desea minimizar o maximizar en función de lo desconocido.
Diferenciar y establecer la derivada igual a cero.
Resuelve y conecte la solución en la función original.
Problemas de posición, velocidad y aceleración
los derivado de la posición es la velocidad y la antiderivada de la velocidad es la posición.
los derivado es la aceleración de la velocidad y de la antiderivada de la aceleración es la velocidad.
Las tasas de los problemas relacionados
Asigne a las variables cambiar cantidades, pero no a inmutable cosas.
Diferenciar antes de enchufar valores de las variables.
Use el teorema de Pitágoras para los problemas de triángulo recto y utilizar triángulos semejantes para los problemas relacionados con conos o formas que tienen una sección transversal triangular.
Cálculo: Técnicas de Integración
Usted encontrará que hay muchas maneras de resolver un problema de integración en cálculo. La siguiente lista contiene algunos puntos prácticos para recordar cuando se utilizan diferentes técnicas de integración:
Adivina y Check. Esta técnica funciona cuando el integrando es cerca de un simple derivado hacia atrás.
u-sustitución. La contraparte de integración a la cadena REGLA utilizar esta técnica cuando el argumento de la función que está integrando es más que un simple X.
Integración por partes. Contraparte de Integración a la regla del producto.
1. Utilice esta técnica cuando el integrando contiene un producto de funciones.
2. Escoja su u según LIATE, cuadro que, "7" que, terminarlo.
Trig Integrales
1. Uso identidades pitagóricas.
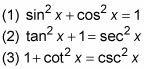
2. Utilice fórmulas medio ángulo.
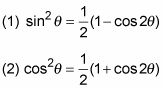
Sustitución trigonométrica. Este método funciona cuando el integrando contiene radicales de las formas
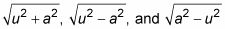
(o poderes de estas raíces), donde la es una constante y u es una expresión en X.
Fracciones parciales. Esta técnica funciona para las funciones racionales (un polinomio sobre otra).
Resolver Problemas de Integración en Cálculo
Cálculo acertijo: ¿Qué teorema del valor medio, la lavadora y Métodos de Shell, y la longitud del arco y de la superficie de las fórmulas de la revolución tienen en común? Todos ellos implican la integración. La integración es además muy elegante. Al resolver un problema de la integración, se toma una forma extraña cuya área no puede determinar directamente, entonces se corta para arriba en pequeños trozos cuyas áreas que poder determinar, y, por último, se suman todos estos pequeños trozos para determinar el conjunto.
Entendiendo el Infinito en Cálculo
En cálculo, un serie infinita es "simplemente" la suma de todos los términos en una secuencia infinita. A pesar de que se suman un número infinito de términos, algunas de estas series en total hasta un número finito ordinaria. Estas series se dice que converger. Si una serie no converge, se dice que divergir. Si una serie converge o diverge es uno de los primeros y más importantes cosas que usted querrá para determinar sobre la serie.
He aquí un vistazo a varios métodos que puede utilizar para probar la convergencia o divergencia de una serie infinita.
nprueba ª plazo: Si el n-ésimo término de una serie no converge a cero, la serie diverge.
Serie geométrica:
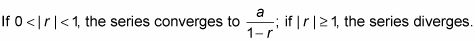
p-serie:
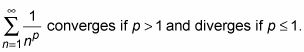
Prueba de razón:
Prueba de raíz:
Prueba de comparación directa: Si la serie dada es más pequeño que su serie de referencia convergente, entonces la serie dada converge también- si la serie dada es más grande que su serie de referencia divergente, entonces la serie dada diverge también.
Prueba de comparación Integral: Si la integral converge impropias de referencia, también lo hace el ídem en serie dada de divergencia.
Limite la prueba de comparación: Para dos series
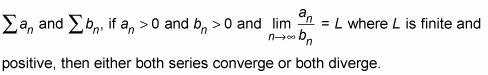
Alternando prueba de la serie: Una serie alternada converge si
1. Su nº término converge a cero.
2. Cada término es inferior o igual al término anterior (ignorando los signos negativos).
Cómo analizar una serie telescópica
Cómo analizar la convergencia absoluta y condicional
Cómo analizar una serie p
Cómo determinar los límites de secuencias con l'h & # 244-pital gobierno de
Cómo determinar si una serie alternante converge o diverge
¿Cómo reconocer una serie p
¿Cómo resolver integrales impropias de funciones que tienen asíntotas verticales
¿Cómo resolver integrales impropias que tienen uno o dos límites infinitos de integración
Cómo comprobar si una serie converge o diverge
Cómo utilizar la prueba de comparación límite para determinar si una serie converge
Cómo utilizar la prueba enésimo plazo para determinar si una serie converge
Cómo utilizar la prueba de raíz para determinar si una serie converge