¿Cómo resolver integrales impropias que tienen uno o dos límites infinitos de integración
Una de las formas en que pueden ser integrales definidas inadecuada es cuando uno o ambos de los límites de integración son infinitas. A resolver este tipo de integral impropia al convertirlo en un problema de límite en c tiende a infinito o infinito negativo. He aquí dos ejemplos:
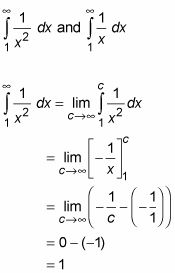
Debido a que esta integral impropia tiene una respuesta finita, que decir que converge.
Convergencia y Divergencia: Una integral impropia converge si existe el límite, es decir, si el límite es igual a un número finito. De lo contrario, se dice que una integral impropia de divergir.
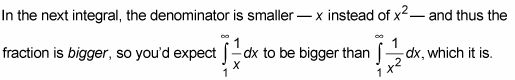
Pero no es sólo más grande, es camino, camino más grande.
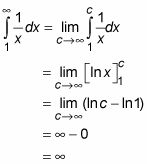
Esta integral impropia diverge.
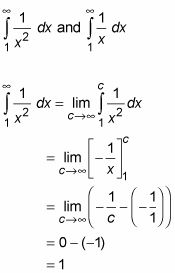
La figura anterior muestra estas dos funciones.
Sus formas son muy similares, pero sus áreas no podrían ser más diferentes.
Vamos a pasar a algo un poco más complicado. Cuando ambos de los límites de integración son infinitos, dividir la integral en dos y encender cada parte en un límite. Dividir la integral en X = 0 es conveniente porque cero es un número fácil de tratar, pero se puede dividir en cualquier lugar que desee. Zero también podría parecer una buena opción, ya que parece que está en el medio entre menos infinito y el infinito. Pero eso es una ilusión, porque no hay medio entre menos infinito y el infinito, o usted podría decir que cualquier punto de la X-eje es el medio.
He aquí un ejemplo:
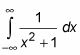
Dividir la integral en dos.
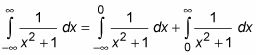
Gire cada parte en un límite.
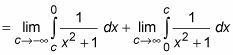
Evaluar cada parte y sumar los resultados.
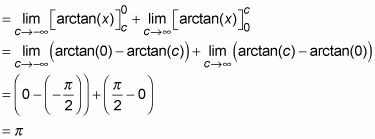
Bastante respuesta fresco, ¿eh?
Si cualquiera " media " integral diverge, el conjunto diverge. No se puede, por ejemplo, obtener el infinito por una infinidad integral y negativo para el otro, y luego sumarlos para obtener cero.
La evaluación de las integrales triples Integrales triples son generalmente integrales definidas, por lo que la evaluación de los resultados en un número real. La evaluación de las integrales triples es similar a la evaluación de funciones anidadas: Usted trabaja de adentro hacia…
Encuentra las zonas exactas bajo una curva mediante la integral definida Cuando se aproxima el área bajo una curva utilizando rectángulos, los más rectángulos que utiliza la izquierda, derecha, o punto medio, mejor será la aproximación. Por lo tanto, "todos" que tendría que hacer para conseguir el área exacta…
Cómo evaluar una integral impropia que es horizontalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA horizontalmente infinita integral impropia contiene ya sea # 8734- o - # 8734- (o ambos) como un límite de la integración.Evaluación de una integral impropia es un…
Cómo evaluar una integral impropia que es verticalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA verticalmente infinita integral impropia contiene al menos una asíntota vertical. Verticalmente integrales impropias infinitos son más difíciles de reconocer que los que…
¿Cómo resolver un problema de límite de plug-and-chu Algunos problemas de límite, como los problemas de plug-and-chug, son muy fáciles de resolver. Sólo tiene que conectar el número de flecha en la función de límite, y si los resultados de cálculo de un número, esa es su respuesta (pero ver la…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
¿Cómo resolver integrales impropias de funciones que tienen asíntotas verticales A resolver integrales impropias, al convertirlos en problemas de límite. No se puede hacer de ellos la manera regular. He aquí cómo resolver integrales impropias de funciones que tienen asíntotas verticales. Hay dos casos: una asíntota vertical…
¿Cómo resolver los límites en el infinito con una calculadora Despejando límites en el infinito es fácil de hacer cuando se utiliza una calculadora. Por ejemplo, escribir la función debajo en el modo de gráficos de la calculadora:entonces ve a tpoder setup y establecer TblStart a 100.000 y # 8710-Tbl a…
¿Cómo resolver los límites en el infinito mediante el uso de asíntotas horizontales Asíntotas horizontales y límites en el infinito siempre van de la mano. No se puede tener uno sin el otro. Si usted tiene una función racional comodeterminar el límite en el infinito o infinito negativo es lo mismo que encontrar la ubicación de…
Cómo dividir una integral definida en dos integrales definidas Cuando la solución de problemas de la zona, a veces es necesario dividir una integral en dos integrales definidas separadas. Aquí hay una regla simple, pero muy útil para hacer esto que parece complicado, pero es realmente muy fácil:Esta regla…
Cómo utilizar la prueba de comparación límite para determinar si una serie converge La idea detrás de la prueba de comparación de límite es que si usted toma una serie convergente conocido y se multiplica cada uno de sus términos por algún número, luego que la nueva serie también converge. Y no importa si el multiplicador…
La medición de volumen bajo una superficie usando una integral doble Una integral doble le permite medir el volumen bajo una superficie tan limitada por un rectángulo. Integrales definidas proporcionan una forma confiable de medir el área firmado entre una función y la X-eje como limitada por cualquiera de los dos…