Cómo identificar un término en una secuencia geométrica cuando sabes mandatos consecutivos
Si tu profesor de pre-cálculo le da mandatos consecutivos en una secuencia geométrica y le pide que identifique un nuevo mandato en la secuencia, los pasos que deberá seguir para encontrar este término son muy similares a los de las secuencias aritméticas. Usted encontrará la razón común (no la diferencia!), Se escribe la fórmula específica para la secuencia dada, y entonces usted encuentra el término que está buscando.
Un ejemplo de una secuencia geométrica es 2, 4, 8, 16, 32. Para hallar el decimoquinto plazo, siga estos pasos:
Encuentra la razón común, r.
En esta secuencia, cada mandato consecutivo es el doble de la anterior legislatura. Si usted no puede ver la razón común examinado la secuencia, dividir cualquier término por el término antes.
Encontrar la fórmula para la secuencia dada.
En términos de la fórmula, la1 = 2 y r = 2. La fórmula general para esta secuencia es
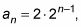
que simplifica (usando las reglas de los exponentes) a
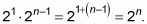
Encontrar el término que está buscando.
Si lan = 2n, después la15 = 215 = 32.768.
La fórmula en este ejemplo simplifica muy bien debido a que las bases de los dos exponentes son los mismos. Si el primer plazo y r no tienen la misma base, no se puede combinarlos.





