¿Cómo encontrar el enésimo término utilizando los primeros términos de una progresión aritmética
Si conoces a los primeros términos de una progresión aritmética, puede escribir una expresión general para la secuencia para encontrar el nº plazo. Para escribir la expresión general, debe buscar un patrón en los primeros términos de la sucesión, lo que demuestra el pensamiento lógico (y todos queremos ser pensadores lógicos, ¿verdad?). La fórmula se escribe debe trabajar para cada valor entero de n, empezando con n = 1.
A veces, este cálculo es una tarea fácil, ya veces es menos evidente y más complicado. Secuencias que implican fracciones y / o exponentes tienden a ser más complicada y menos evidente en sus patrones. Los más fáciles de escribir incluyen la suma, resta, multiplicación o división por números enteros.
Por ejemplo, para encontrar la fórmula general para la nº término de la sucesión 2/3, 3/5, 4/7, 9/5, 6/11, usted debe buscar en el numerador y el denominador por separado:
Los numeradores comienzan con 2 y aumentan en uno cada vez. Esta secuencia se describe por lan = n + 1.
Los denominadores comienzan con 3 y aumentan por dos cada vez. Esta secuencia se describe por lan = 2n + 1.
Por lo tanto, esta secuencia puede ser expresada por esta fórmula general:
Para corroborar su fórmula y asegurar que las respuestas funcionan, tapón en 1, 2, 3, y así sucesivamente para asegurarse de obtener los números originales de la secuencia dada.
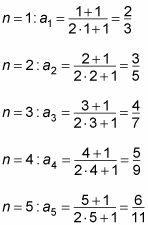
Todos ellos trabajan, por lo que lo hiciste bien!
-
Cómo entrar en una secuencia en la TI-83 Plus -
Guardar y dibujar gráficos de secuencia en la TI-83 Plus -
Cómo introducir secuencias en la TI-84 Plus -
Cómo graficar una sucesión recursiva en la TI-84 Plus -
Recicle respuestas y las entradas anteriores con la TI-84 Plus calculadora -
Cómo generar datos secuenciales en la TI-Nspire
Cómo utilizar la última respuesta en la TI-Nspire Cada vez que realice un cálculo, el resultado se almacena en la memoria local de TI-Nspire como la variable Ans. Como resultado, se puede acceder rápidamente a esta variable almacenada y utilizarla en cálculos posteriores.Considere, por ejemplo,…
Comparando convergentes y divergentes secuencias Cada secuencia infinita es ya sea convergente o divergente. LA convergente secuencia tiene un límite - es decir, que se aproxima a un número real. LA divergente secuencia no tiene un límite.He aquí un ejemplo de una secuencia convergente:Esta…
Cómo calcular los términos de un secuencia mediante el uso de la expresión secuencia Si te dan unos términos de una secuencia, a menudo se pueden usar estos términos para encontrar la fórmula general para la secuencia. Si te dan la fórmula general (completo con n como la variable), se encuentra el nº término de la sucesión…
Cómo determinar los límites de secuencias con l'h & # 244-pital gobierno de Usted puede utilizar la regla de L'H # de 244-pital de encontrar límites de sucesiones. Regla de L'H # de 244-pital es un gran atajo para cuando haces limitar problemas. Aquí está:Convergencia y Divergencia: Usted dice que una secuencia converge…
¿Cómo encontrar la fórmula general para el enésimo término de una sucesión aritmética utilizando cualquiera de los dos términos En algún momento, su profesor de pre-cálculo le pedirá que encontrar la fórmula general para la nº período de una sucesión aritmética sin conocer el primer término o la diferencia común. En este caso, se le dará dos términos (no…
¿Cómo encontrar la suma parcial de una secuencia aritmética Cuando su profesor de pre-cálculo pide a calcular la kº suma parcial de una secuencia aritmética, es necesario agregar el primer k términos. Esto puede tardar un poco, sobre todo si k es largo. Afortunadamente, usted puede utilizar una fórmula…
¿Cómo encontrar la suma parcial de una secuencia geométrica Cuando su profesor de pre-cálculo le pide que encontrar la suma parcial de una secuencia geométrica, la suma tendrá un límite superior y un límite inferior. La razón común de sumas parciales de este tipo no tiene restricciones…
¿Cómo encontrar el valor de una suma infinita en una secuencia geométrica Si tu profesor de pre-cálculo le pide que encontrar el valor de una suma infinita en una secuencia geométrica, el proceso es muy simple - siempre y cuando usted mantenga sus fracciones y decimales recta. Si r se encuentra fuera del rango -1 lt; r…
Cómo identificar un término en una secuencia geométrica cuando sabes mandatos consecutivos Si tu profesor de pre-cálculo le da mandatos consecutivos en una secuencia geométrica y le pide que identifique un nuevo mandato en la secuencia, los pasos que deberá seguir para encontrar este término son muy similares a los de las secuencias…
Cómo identificar un término en una secuencia geométrica cuando sabes dos mandatos no consecutivos Si tu profesor de pre-cálculo le da dos términos no consecutivos de una secuencia geométrica, se puede encontrar la fórmula general de la secuencia, así como cualquier término especificado. Por ejemplo, si el quinto término de una secuencia…
¿Cómo reconocer secuencias aritméticas recursivas LA secuencia recursiva es una secuencia aritmética en la que cada término depende del plazo (s) antes de IT- la secuencia de Fibonacci es un ejemplo bien conocido. Cuando su profesor de pre-cálculo le pide que encontrar cualquier término en una…
Cómo usar términos consecutivos de encontrar otro en una secuencia aritmética Si tu profesor de pre-cálculo le da dos términos consecutivos de una progresión aritmética y le pide que encontrar otro, puede utilizar una fórmula general para encontrar la diferencia común entre estos términos. Por ejemplo, una secuencia…