¿Cómo encontrar la fórmula general para el enésimo término de una sucesión aritmética utilizando cualquiera de los dos términos
En algún momento, su profesor de pre-cálculo le pedirá que encontrar la fórmula general para la nº período de una sucesión aritmética sin conocer el primer término o la diferencia común. En este caso, se le dará dos términos (no necesariamente consecutivos), y que va a utilizar esta información para encontrar la1 y d. Los pasos son: Encuentre la diferencia común d, escribir la fórmula específica para la secuencia dada, y luego encontrar el término que está buscando.
Por ejemplo, para encontrar la fórmula general de una progresión aritmética, donde la4 = -23 Y la22 = 40, siga estos pasos:
Encuentra la diferencia común.
Tienes que ser creativos en la búsqueda de la diferencia común para este tipo de problemas.
a.Utilice la fórmula lan = la1 + (n - 1)d la creación de dos ecuaciones que utilizan la información dada.
Por primera ecuación, ya sabes que cuando n = 4, lan = -23:
-23 = la1 + (4 - 1)d
-23 = la1 + 3d
Para la segunda ecuación, ya sabes que cuando n = 22, lan = 40:
40 = la1 + (22 - 1)d
40 = la1 + 21d
b.Set un sistema de ecuaciones y resolver d.
El sistema se ve así:
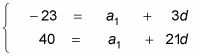
Puede usar la eliminación o sustitución para resolver el sistema. Eliminación funciona muy bien, porque se puede multiplicar ya sea ecuación por -1 y añadir los dos juntos para conseguir 63 = 18d. Por Consiguiente, d = 3,5.
Escribe la fórmula para la secuencia específica.
Este paso implica un poco de trabajo.
un enchufe d en una de las ecuaciones para resolver de la1.
Puede conectar 3.5 de nuevo en cualquiera de las ecuaciones:
-23 = la1 + 3 (3,5), o la1 = -33,5.
b.Utilice la1 y d para encontrar la fórmula general para lan.
Este paso se convierte en una sencilla simplificación de tres pasos:
lan = -33,5 + (n - 1) 3.5
lan = -33,5 + 3,5n - 3.5
lan = 3,5n - 37
Encontrar el término que estás buscando.
En este ejemplo, no se le pidió para encontrar cualquier término específico (siempre lea las instrucciones!), Pero si lo fuera, se podría conectar ese número por n y luego encontrar el término que estás buscando.
-
Cómo graficar una sucesión recursiva en la TI-84 Plus -
1,001 Álgebra practico problemas para los maniquíes - Encontrar las intersecciones de las líneas y las parábolas
-
Resolver dos ecuaciones lineales algebraicamente -
Los sistemas con tres ecuaciones lineales - Los fundamentos de la resolución de ecuaciones de álgebra i
Encontrar las raíces de una ecuación factorizada En pre-cálculo, puede utilizar la propiedad del producto cero a encontrar las raíces de una ecuación factorizada. Después se toma un polinomio en sus diferentes piezas, puede configurar cada pieza igual a cero para resolver las raíces con la…
Cómo calcular los términos de un secuencia mediante el uso de la expresión secuencia Si te dan unos términos de una secuencia, a menudo se pueden usar estos términos para encontrar la fórmula general para la secuencia. Si te dan la fórmula general (completo con n como la variable), se encuentra el nº término de la sucesión…
¿Cómo encontrar el enésimo término utilizando los primeros términos de una progresión aritmética Si conoces a los primeros términos de una progresión aritmética, puede escribir una expresión general para la secuencia para encontrar el nº plazo. Para escribir la expresión general, debe buscar un patrón en los primeros términos de la…
¿Cómo encontrar la suma parcial de una secuencia aritmética Cuando su profesor de pre-cálculo pide a calcular la kº suma parcial de una secuencia aritmética, es necesario agregar el primer k términos. Esto puede tardar un poco, sobre todo si k es largo. Afortunadamente, usted puede utilizar una fórmula…
Cómo identificar un término en una secuencia geométrica cuando sabes mandatos consecutivos Si tu profesor de pre-cálculo le da mandatos consecutivos en una secuencia geométrica y le pide que identifique un nuevo mandato en la secuencia, los pasos que deberá seguir para encontrar este término son muy similares a los de las secuencias…
Cómo identificar un término en una secuencia geométrica cuando sabes dos mandatos no consecutivos Si tu profesor de pre-cálculo le da dos términos no consecutivos de una secuencia geométrica, se puede encontrar la fórmula general de la secuencia, así como cualquier término especificado. Por ejemplo, si el quinto término de una secuencia…
¿Cómo reconocer secuencias aritméticas recursivas LA secuencia recursiva es una secuencia aritmética en la que cada término depende del plazo (s) antes de IT- la secuencia de Fibonacci es un ejemplo bien conocido. Cuando su profesor de pre-cálculo le pide que encontrar cualquier término en una…
¿Cómo resolver una ecuación cuadrática cuando no lo hará factor de Cuando se le preguntó a resolver una ecuación cuadrática que usted apenas no puede parecerse al factor (o que simplemente no hace de los factores), hay que emplear otras formas de resolver la ecuación, como mediante el uso de la fórmula…
¿Cómo resolver sistemas lineales que tienen más de dos ecuaciones Cuando su instructor de pre-cálculo le pide que resolver grandes sistemas de ecuaciones lineales, estas ecuaciones involucrarán más de dos ecuaciones que van junto con más de dos variables. Usted puede escribir estos sistemas más grandes de la…
¿Cómo resolver sistemas no lineales En un sistema no lineal, al menos una ecuación tiene una gráfica que no es una línea recta - es decir, al menos una de las ecuaciones tiene que ser no lineal. Su instructor de pre-cálculo le dirá que siempre se puede escribir una ecuación…
Cómo usar términos consecutivos de encontrar otro en una secuencia aritmética Si tu profesor de pre-cálculo le da dos términos consecutivos de una progresión aritmética y le pide que encontrar otro, puede utilizar una fórmula general para encontrar la diferencia común entre estos términos. Por ejemplo, una secuencia…
Sistemas de ecuaciones utilizadas en pre-cálculo LA sistema de ecuaciones es una colección de dos o más ecuaciones que implican dos o más variables. Si el número de ecuaciones es igual al número de variables diferentes, entonces usted puede ser capaz de encontrar una solución única que es…