¿Cómo encontrar la suma parcial de una secuencia aritmética

categoría Educación y lenguas / Matemáticas / Cálculo

Cuando su profesor de pre-cálculo pide a calcular la kº suma parcial de una secuencia aritmética, es necesario agregar el primer k términos. Esto puede tardar un poco, sobre todo si k es largo. Afortunadamente, usted puede utilizar una fórmula en lugar de conectar cada uno de los valores para n. los ksuma parcial º de una serie aritmética es

image0.jpg

Sólo tiene que enchufar los límites inferior y superior en la fórmula lan encontrar la1 y lak.

Secuencias aritméticas son muy útiles para identificar debido a que la fórmula para el nº término de una secuencia aritmética es siempre la misma:

lan = la1 + (n - 1)d

dónde la1 es el primer plazo y d es la diferencia común.

Una de las aplicaciones del mundo real de una suma aritmética implica asientos del estadio. Digamos, por ejemplo, el estadio tiene 35 filas de asientos- hay 20 asientos en la primera fila, 21 asientos en la segunda fila, 22 asientos en la tercera fila, y así sucesivamente. ¿Cuántos asientos contienen todas las 35 filas? Siga estos pasos para averiguar:

  1. Encuentra el primer término de la sucesión.

    El primer término de esta secuencia (o el número de asientos en la primera fila) se da: 20.

  2. Encuentra el kº término de la sucesión.

    Debido a que el estadio tiene 35 filas, encontrar la35. Use la fórmula para el nº término de una secuencia aritmética. El primer término es 20, y cada fila tiene un escaño más que la fila antes de que, por lo d = 1. Conecte estos valores en la fórmula:

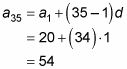
    image1.jpg

    Nota: Esta solución es el número de asientos en la fila 35, no es la respuesta a la cantidad de asientos del estadio contiene.

  3. Use la fórmula para el ksuma parcial º de una sucesión aritmética para encontrar la suma.

    image2.jpg


Artículos Relacionados

Sobre el autor
¿Cómo encontrar la fórmula general para el enésimo término de una sucesión aritmética utilizando cualquiera de los dos términos ¿Cómo encontrar la fórmula general para el enésimo término de una sucesión aritmética utilizando cualquiera de los dos términos

En algún momento, su profesor de pre-cálculo le pedirá que encontrar la fórmula general para la nº período de una sucesión aritmética sin conocer el primer término o la diferencia común. En este caso, se le dará dos términos (no…

¿Cómo encontrar el enésimo término utilizando los primeros términos de una progresión aritmética ¿Cómo encontrar el enésimo término utilizando los primeros términos de una progresión aritmética

Si conoces a los primeros términos de una progresión aritmética, puede escribir una expresión general para la secuencia para encontrar el nº plazo. Para escribir la expresión general, debe buscar un patrón en los primeros términos de la…

¿Cómo encontrar la suma parcial de una secuencia geométrica ¿Cómo encontrar la suma parcial de una secuencia geométrica

Cuando su profesor de pre-cálculo le pide que encontrar la suma parcial de una secuencia geométrica, la suma tendrá un límite superior y un límite inferior. La razón común de sumas parciales de este tipo no tiene restricciones…

¿Cómo encontrar el valor de una suma infinita en una secuencia geométrica ¿Cómo encontrar el valor de una suma infinita en una secuencia geométrica

Si tu profesor de pre-cálculo le pide que encontrar el valor de una suma infinita en una secuencia geométrica, el proceso es muy simple - siempre y cuando usted mantenga sus fracciones y decimales recta. Si r se encuentra fuera del rango -1 lt; r…

Cómo identificar un término en una secuencia geométrica cuando sabes mandatos consecutivos Cómo identificar un término en una secuencia geométrica cuando sabes mandatos consecutivos

Si tu profesor de pre-cálculo le da mandatos consecutivos en una secuencia geométrica y le pide que identifique un nuevo mandato en la secuencia, los pasos que deberá seguir para encontrar este término son muy similares a los de las secuencias…

Cómo identificar un término en una secuencia geométrica cuando sabes dos mandatos no consecutivos Cómo identificar un término en una secuencia geométrica cuando sabes dos mandatos no consecutivos

Si tu profesor de pre-cálculo le da dos términos no consecutivos de una secuencia geométrica, se puede encontrar la fórmula general de la secuencia, así como cualquier término especificado. Por ejemplo, si el quinto término de una secuencia…

¿Cómo reconocer secuencias aritméticas recursivas ¿Cómo reconocer secuencias aritméticas recursivas

LA secuencia recursiva es una secuencia aritmética en la que cada término depende del plazo (s) antes de IT- la secuencia de Fibonacci es un ejemplo bien conocido. Cuando su profesor de pre-cálculo le pide que encontrar cualquier término en una…

Cómo usar términos consecutivos de encontrar otro en una secuencia aritmética Cómo usar términos consecutivos de encontrar otro en una secuencia aritmética

Si tu profesor de pre-cálculo le da dos términos consecutivos de una progresión aritmética y le pide que encontrar otro, puede utilizar una fórmula general para encontrar la diferencia común entre estos términos. Por ejemplo, una secuencia…

Cómo utilizar la notación de sumatoria para mostrar una suma parcial de una secuencia Cómo utilizar la notación de sumatoria para mostrar una suma parcial de una secuencia

Notación de sumatoria es una forma útil para representar la suma parcial de una secuencia. La suma de la primera k términos de una progresión aritmética se conoce como la ksuma parcial TH. Se llaman sumas parciales porque sólo eres capaz de…

Velocidad, distancia y tiempo de preguntas de la prueba de aritmética Velocidad, distancia y tiempo de preguntas de la prueba de aritmética

Las preguntas típicas distancia en tiempo de velocidad en las pruebas de aritmética piden que resolver una de las tres cantidades, dado que los otros dos. Se puede ver que la velocidad está relacionada con la distancia y el tiempo si sólo…

¿Cómo encontrar la media aritmética ponderada de un conjunto de datos ¿Cómo encontrar la media aritmética ponderada de un conjunto de datos

A veces, un conjunto de datos contiene un gran número de valores repetidos. En estas situaciones, se puede simplificar el proceso de cálculo de la media mediante el uso de pesos - las frecuencias de un valor en una muestra o una población. Puede…

Averiguar fracciones durante la prueba de aritmética Averiguar fracciones durante la prueba de aritmética

No deje que las fracciones zorro usted! Cuando usted está revisando para su prueba de aritmética, siga estos pasos rápidos y sencillos para añadir o para llevar dos fracciones:Multiplicar la parte superior e inferior de la primera fracción por…

» » » » ¿Cómo encontrar la suma parcial de una secuencia aritmética