Cómo trabajar y verificar integral de convolución y resumir los problemas

El dominio de las integrales de convolución y sumas viene a través de la práctica. Aquí hay soluciones detalladas de análisis a un solo integral de convolución y dos sumas de convolución problemas, cada uno seguido de verificaciones numéricos detallados, utilizando PyLab del shell interactivo IPython (la versión de QT en particular).

Convolución en tiempo continuo

He aquí un ejemplo integral de convolución empleando señales de medida semi-infinitos. Considere la convolución de X(t) = u(t) (Una función escalón unitario) y

(un verdadero decaimiento exponencial a partir de t = 0). La figura proporciona un gráfico de las formas de onda.

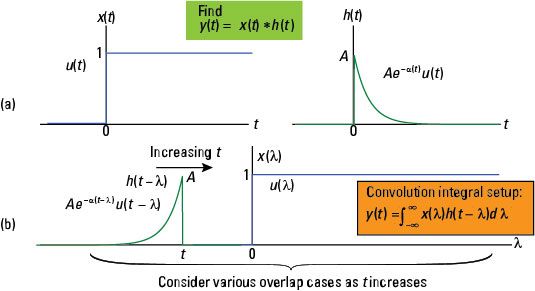
El intervalo de soporte de salida es

Se necesitan dos casos (pasos) para formar la solución analítica válida en todo el eje de tiempo.

• Caso 1: Utilizando la figura b, se puede ver claramente que para t lt; 0, se deduce que y(t) = 0.

• Caso 2: Una vez más mirando a la figura b, se ve que para t # 8805- 0, cierta superposición siempre se produce entre las dos señales del integrando. La salida integral de convolución es

  

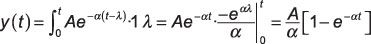
Poner las dos piezas juntas, la solución analítica para y(t) es

Para verificar esta solución analítica, siga los mismos pasos que utilizó en el ejemplo anterior:

1. Escriba una función Python simple para trazar la solución analítica:

   En [133]: Def expo_conv (t, A, alfa): ...: y = ceros (len (t)) ...: para k, tk en enumerate (t): ...: si tk> = 0 :. ..: y [k] = A / alfa * (1 - exp (-alfa * tk)) ...: retorno y

2. Para la convolución numérica, el uso ssd.conv_integral (). En primer lugar, escribir código Python en la ventana de comandos para generar las señales X(t) Y h(t) Y luego llevar a cabo la convolución:

   En [135]: T = arange (-4,14, 0,01) En [136]: Xc2 = ssd.step (t) En [137]: Hc2 = ssd.step (t) * exp (-1 * t) En [138]: Yc2_num, tyc2 = ssd.conv_integral (xc2, t, hc2, t, ('r', 'r')) Soporte de salida: (-8.00, 5.99) En [143]: Subtrama (211) En [144]: Plot (t, expo_conv (t, 1,1)) En [149]: Subtrama (212) En [151]: Plot (tyc2, yc2_num) En [156]: Savefig ('c2_outputs.pdf')

   Observe que el quinto argumento de la conv_integral función es ('r', 'r'). Para señales con extensión infinita a la derecha, cada uno 'r' cuenta la función que ambas señales están en lo cierto; lados y para devolver sólo el intervalo de soporte válido bajo este supuesto.

   Los valores por defecto de ('f', 'f') significa soporte finito para ambas señales a través de los ejes de tiempo de entrada t1 y t2 dada a la función.

   

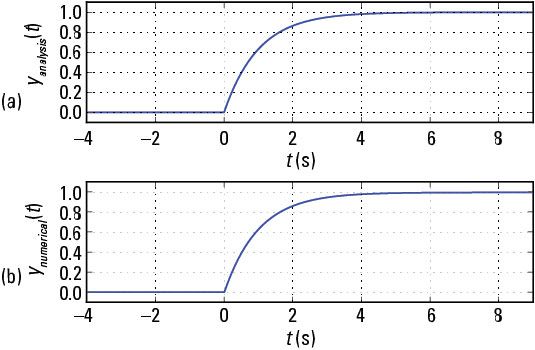
Una vez más, el acuerdo es excelente, por lo que la solución analítica se verifica.

Verifique convolución de tiempo discreto

Para el caso de convolución discreta, aquí hay dos ejemplos de suma de convolución. El primero emplea secuencias de extensión finita (señales) y el segundo emplea señales de medida semi-infinitos. Se encuentra con los dos tipos de secuencias en la resolución de problemas, pero medida secuencias finitas es el punto de partida habitual cuando estás primero trabajando con la suma de convolución.

Dos secuencias de longitud finita

Tenga en cuenta la suma de convolución de las dos secuencias X[n] Y h[n], Que se muestra aquí, junto con la configuración de la suma de convolución.

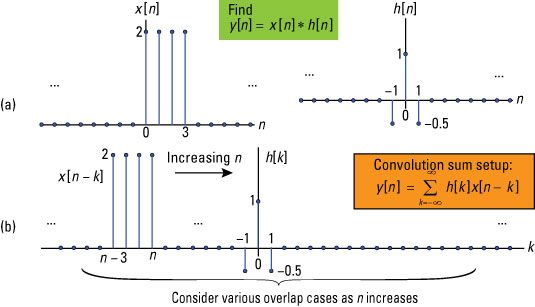
Cuando convolución de secuencias de duración finita, puede hacerlo la solución analítica casi por inspección o tal vez mediante el uso de una tabla (incluso una hoja de cálculo) para organizar los valores de secuencia para cada valor de n, que produce un solapamiento entre distinto de cero h[k] Y X[n - k].

El intervalo de apoyo a la salida sigue la regla dada por el dominio de tiempo continuo. La salida y[n] Comienza a la suma de los dos puntos de partida de la secuencia de entrada y termina a la suma de la secuencia de entrada terminando puntos. Para el problema en cuestión corresponde a y[n] A partir de [0 + -1] = -1 y termina en [3 + 1] = 4.

En cuanto a la figura b, se puede ver que a medida n aumenta desde n lt; -1, Primero solapamiento se produce cuando n = -1. El último punto de coincidencia se produce cuando n - 3 = 1 o n = 4. Puede configurar una tabla de hoja de cálculo para evaluar los productos de suma de seis relacionados con el intervalo de soporte de salida.

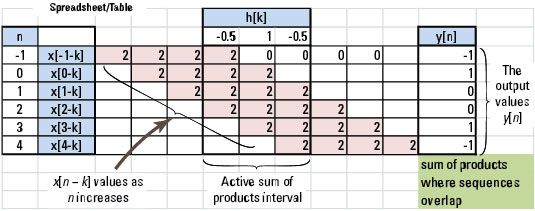
Para verificar estos (hoja de cálculo) Los valores de cálculo de la mano, utilice las funciones de Python en ssd.py para realizar la suma de convolución. La función de suma de convolución es y, ny = ssd.conv_sum (x1, nx1, x2, nx2, medida = ('f', 'f')).

En [208]: N = arange (-4,6) En [209]: Xd1 = 2 * ssd.drect (n, 4) En [210]: Hd1 = 1,5 * ssd.dimpulse (n) - 0,5 * ssd.drect (n + 1,3) En [211]: Yd1_num, nd1 = ssd.conv_sum (xd1, n, hd1, n) el apoyo de la salida: (-8, 10) En [212]: Tallo (nd1, yd1_num)

Ver la secuencia de salida resultados numérica traza.

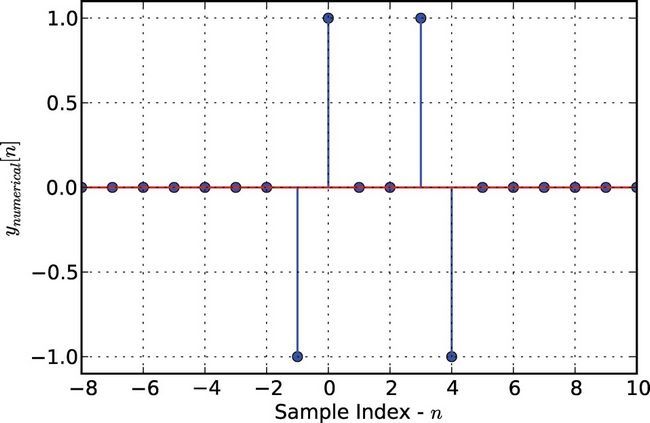
Los resultados del cálculo numérico de hecho se corresponden con el cálculo mano.

Uno finito y una secuencia semi-infinito

Como un segundo ejemplo de trabajo con la convolución considerar una secuencia de pulsos de duración finita 2M + 1 puntos convolucionados con la secuencia exponencial semi-infinita laⁿ u[n] (Un verdadero decaimiento exponencial a partir de n = 0). Una parcela de las formas de onda se da aquí.

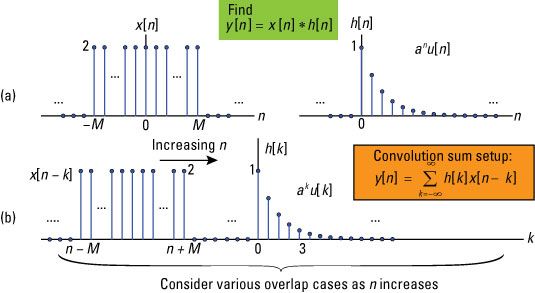
Con la ayuda de la figura b, tiene tres casos a considerar en la evaluación de la convolución para todos los valores de n. El intervalo de apoyo a la convolución es

Estos son los pasos para cada caso:

• Caso 1: De la figura b, se ve que para n + M lt; 0 o n lt; -M no se produce solapamiento entre las dos secuencias de la suma, por lo y[n] = 0.

• Caso 2: Superposición parcial entre las dos secuencias se produce cuando n + M # 8805- 0 y n - M # 8804- 0 o -M # 8804- n # 8804- M. Los límites de suma comienzan en k = 0 y terminan a las k = n + M. Utilizando la fórmula de suma serie geométrica finita, la suma de convolución se evalúa como

  

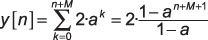
• Caso 3: Superposición completa se produce cuando n - M > 0 o n > M. Los límites de sumas menores de este caso van desde k = n - M a k = n + M. Una vez más, utilizando la fórmula de suma serie geométrica finita, la suma de convolución se evalúa como

  

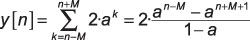
Juntando las piezas, la solución analítica completa para este problema es

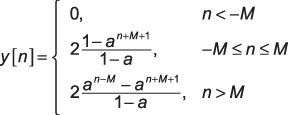
Comparar la solución analítica con la solución numérica, sigue los pasos de trazado de la función analítica en contra de una parcela de la suma de convolución real:

1. Escriba una función de Python para evaluar y[n] Como una función a trozos:

   En [239]: Def expo_pulse_conv (n, a, M): ...: y = ceros (len (n)) ...: para k, nk en enumerate (n): ...: si nk> = -M y nk lt; = M: ...: y [k] = 2 * (1 - a ** (nk + M + 1)) / (1 - a) ...: elif nk> M: ...: y [k] = 2 * (a ** (nk-M) - un ** (nk + M + 1)) / (1 - a) ...: retorno y

2. Encuentra la suma de convolución real mediante el uso de la función conv_sum () y luego graficar los resultados:

   En [255]: N = arange (-5,30) valores # n para x [n] h [n] En [256]: Xd2 = 2 * ssd.drect (n + 4,9) # crear x [n] en [257]: HD2 = ssd.dstep (n) * 0,6 ** n # crean h [n] en [258]: Yd2_num, ND2 = ssd.conv_sum (xd2, n, HD2, n, ('f', 'r')) Soporte de salida: (-10, 24) En [259]: Subtrama (211) En [260]: Tallo (n, expo_pulse_conv (n, 0.6,4)) # analyticalIn [265]: Subtrama (212) En [266]: Tallo (ND2, yd2_num) # numericalIn [271]: Savefig ('d2_outputs.pdf')

   Utilice el quinto argumento a la conv_sum () funcionar para declararán el alcance de la segunda secuencia de entrada a derecha; caras ('r'), en comparación con el valor por defecto de finito ("F"). Esta configuración asegura que la función no devuelve resultados no válidos.

   

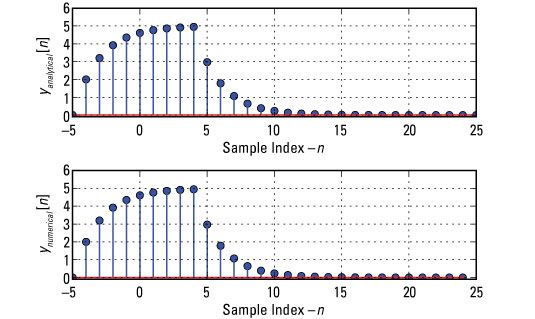
Aquí, se ve que la solución analítica a trozos se compara favorablemente con el cálculo numérico suma de convolución directa.