Cómo comprobar una convolución problema integral numéricamente

Aquí es una solución analítica detallada a un problema integral de convolución, seguido por la verificación numérica detallada, utilizando PyLab desde el shell interactivo IPython (la versión QT en particular). La intención de la solución numérica es demostrar cómo las herramientas informáticas pueden verificar las soluciones analíticas a los problemas de convolución.

Establecer PyLab

Para empezar a utilizar PyLab y el shell interactivo IPython, puede fácilmente configurar las herramientas en Mac OS, Windows y Ubuntu Linux.

Configuración en Ubuntu Linux es quizás el más fácil, ya que sólo puede utilizar el Ubuntu Software Center. En Mac OS y Windows, puede utilizar un instalación monolítica, que instala la mayoría de todo lo que necesita a la vez. Echa un vistazo a la versión gratuita de Enthought, pero otros están disponibles en la web.

Verifique convolución de tiempo continuo

He aquí un ejemplo de convolución empleando señales extensión finita. Soluciones analíticas completas se incluyen, pero la atención se centra en la verificación numérica, en particular, utilizando PyLab y el módulo de código personalizado disponible gratuitamente ssd.py antes mencionado.

Considere la integral de convolución de dos señales de tiempo continuo X(t) Y h(t) mostrado.

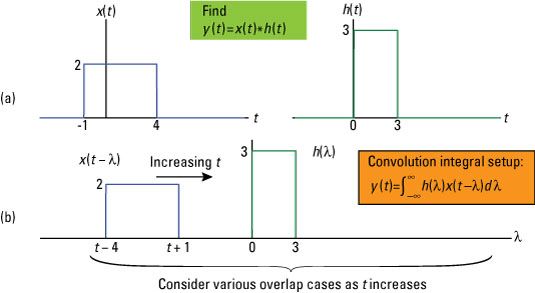
Para llegar a la solución analítica, es necesario romper el problema en cinco casos, o intervalos de tiempo t donde se puede evaluar la integral para formar una solución contigua a trozos. Al poner estos cinco intervalos contiguos entre sí, usted tiene una solución completa para todos los valores de t:

A partir del estudio de las integrales de convolución, se descubre que se puede escribir el apoyo o intervalo activo para los productos y(t) En términos de los intervalos de apoyo para cada una de las señales de entrada. Este resultado indica que el intervalo de soporte de salida va desde la suma de los valores de partida para X(t) Y h(t) Y termina en los valores finales. Por lo tanto, el intervalo de soporte para y(t) Es como máximo

En este ejemplo, cada caso es tratar como un paso en la solución que sigue:

• Caso 1: Se empieza con t + 1 lt; 0, o equivalentemente t lt; -1. El producto de formas de onda h(# 955-) Y X(t - # 955-) no se solapan en la convolución integrando integral, por lo que para el caso 1 la integral es sólo y(t) = 0 para t lt; -1.

• Caso 2: Considere el siguiente intervalo a la derecha de la caja 1. Este caso está formado por la condición conjunta de señal en el borde t + 1 # 8805- 0 y t + 1 lt; 3, que es equivalente a la escritura -1 # 8804- t lt; 2. El integrando de la integral de convolución es 2 x 3 con los límites de integración que va desde 0 a t + 1.

  Tu encuentras y(t) En este intervalo mediante la evaluación de la integral de convolución:

  

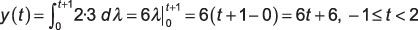
• Caso 3: El siguiente intervalo en la serie es t + 1 # 3 y 8805- t - 4 lt; 0 o 2 # 8804- t lt; 4. El integrando es de nuevo 2 x 3, pero ahora los límites de integración ejecutar desde 0 a 3. Evaluación de los rendimientos de convolución integrales la siguientes:

  

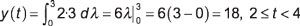
• Caso 4: El intervalo final que implica la superposición de la señal se produce cuando t - 4 # 8805- 0 y t - 4 lt; 3, lo que implica que 4 # 8804- t # 8804- 7. Los límites de integración ejecutan desde t - De 4 a 3, por lo que el resultado integral de convolución es

  

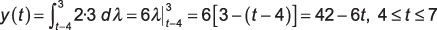
• Caso 5: Se puede ver que cuando t - 4> 3 o t > 7, no se produce solapamiento entre las señales del integrando, por lo que la salida es y(t) = 0, t > 7.

Recopilación de las diferentes piezas de la solución, tiene el siguiente:

Verificación de esta solución con Python implica dos pasos: (1) de trazado de la solución analítica y (2) que comparan con la trama de la solución numérica, utilizando las funciones que se encuentran en el módulo de código ssd.py. Aquí están los detalles para completar estos pasos:

1. Crear una función a trozos en Python que luego se puede evaluar en un rango definido por el usuario de los valores de tiempo.

   Usted puede escribir esta función justo en el shell IPython como se muestra aquí:

   En [68]: Def pulse_conv (t): ...: y = ceros (len (t)) # inicializar matriz de salida ...: para k, tk en enumerate (t): # Haz de Y valores (t) ...: si tk> = -1 y tk lt; 2: ...: y [k] = 6 * tk + 6 ...: elif tk> = 2 y tk lt; 4: ...: y [k] = 18 ...: elif tk> = 4 y tk lt; = 7: ...: y [k] = 42-6 * tk ...: retorno y

   Tenga en cuenta que el lenguaje Python es sensible a los guiones, así que presta atención a los guiones al introducir este código en IPython. La buena noticia es que IPython entiende las necesidades de Python y hace un buen trabajo de sangría bloque de código automáticamente.

2. Numéricamente evaluar la convolución mediante la creación de primera representaciones de las formas de onda reales de la convolución y luego realizar la convolución numérica.

   Para conseguir el acceso a las funciones en el módulo ssd.py, debe importar el módulo en su sesión IPython, utilizando En [69]: ssd importación.

   A continuación, puede acceder a las funciones en el módulo utilizando el prefijo de espacio ssd. La funcion y, ny = ssd.conv_integral (x1, TX1, x2, TX2, medida = ('f', 'f')) realiza la convolución real.

   Usted carga versiones de tiempo de muestreo de las señales que se convolucionados en los argumentos x1 y x2, con tx1 y tx2 siendo los ejes de tiempo correspondientes. Los cuatro de estas variables son NumPy ndarrays. La función devuelve el resultado de convolución y seguido por Nueva York, como una tupla de Python. Las formas de pulsos rectangulares se crean con la función ssd.rect (n, tau) y el eje de tiempo cambiante en los argumentos de la función.

   Poniendo todo junto, el código numérico aproximando el resultado integral de convolución es el siguiente (sólo instrucciones de código críticos se muestran):

   En [89]: T = arange (8,9, 0,01) En [90]: Xc1 = 2 * ssd.rect (t-1.5,5) En [91]: Hc1 = 3 * ssd.rect (t-1.5,3) En [93]: Subtrama (211) En [94]: Plot (t, xc1) En [99]: Subtrama (212) En [100]: Plot (t, hc1) En [101]: Savefig ('c1_intputs.pdf') En [115]: Yc1_num, tyc1 = ssd.conv_integral (xc1, t, hc1, t) el apoyo de la salida: (-16.00, 17.98) En [116]: Subtrama (211) En [117]: Plot (t, pulse_conv (t)) En [123]: Subtrama (212) En [125]: Plot (tyc1, yc1_num) En [130]: Savefig ('c1_outputs.pdf')

   La siguiente figura muestra las parcelas de las señales X(t) Y h(t).

   

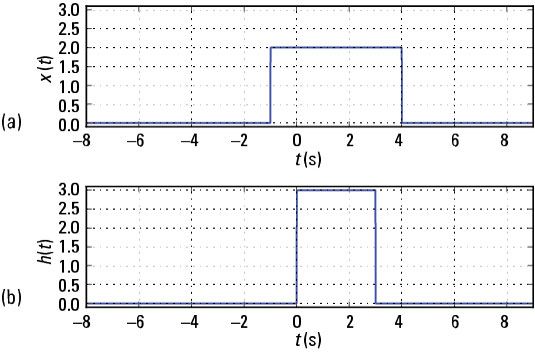
Por último, la representación numérica de y(t) Se representa junto con la solución analítica se muestra.

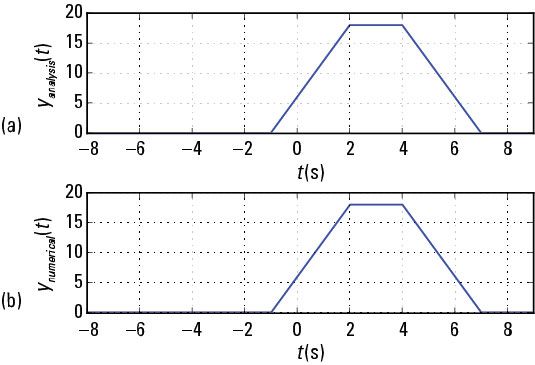
Desde la perspectiva de la trama, las dos soluciones están de acuerdo, por lo que se confirma la solución analítica.