10 Señales y propiedades de sistemas que nunca quiero olvidar

Un gran mundo de las propiedades se asocia con señales y sistemas - un montón en las matemáticas solo! He aquí diez propiedades inolvidables relacionados con las señales y sistemas de trabajo.

La estabilidad del sistema LTI

Tiempo-invariante lineal sistemas (LTI) son entradas delimitada-salida acotada (BIBO) estable si la región de convergencia (ROC) en el s- y zaviones incluye la

los s-avión se aplica a sistemas de tiempo continuo, y el zplano se aplica a los sistemas de tiempo discreto. Pero aquí está la parte fácil: Para los sistemas causales, la propiedad es polos en el izquierdo; media s-avión y polos en el interior del círculo unidad del zavión.

Convolución de rectángulos

La convolución de dos pulsos o secuencias de forma rectangular idénticos resulta en un triángulo. El pico del triángulo se encuentra en la integral de la señal o la suma de la secuencia de cuadrado.

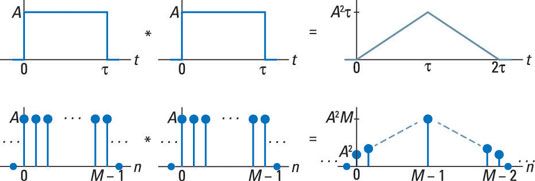
El teorema de convolución

Los cuatro (lineales) teoremas de convolución son transformada de Fourier (FT), en tiempo discreto transformada de Fourier (DTFT), transformada de Laplace (LT), y z-transformación (ZT).Nota: El tiempo discreto transformada de Fourier (DFT) no cuenta aquí porque convolución circular es un poco diferente de los demás en este conjunto.

Estos cuatro teoremas tienen el mismo resultado poderosa: convolución en el dominio del tiempo se puede reducir a la multiplicación en los dominios respectivos. por X₁ y X₂ señal o respuesta de impulso, y = X_{1 *} X₂ se convierte en

Magnitud Respuesta de frecuencia

Para los dominios continuous- y de tiempo discreto, la magnitud de respuesta de frecuencia de un sistema LTI está relacionada con la geometría de polos y ceros.

Para las señales de tiempo continuo, se trabaja en el s-dominio- si el sistema es estable, se obtiene la magnitud de respuesta de frecuencia mediante la evaluación | H (s) | a lo largo de j# 969--eje.

Para las señales de tiempo discreto, se trabaja en el zdominio- si el sistema es estable, se obtiene la magnitud de respuesta de frecuencia mediante la evaluación | H (z) | alrededor del círculo unidad,

En ambos casos, la anulación magnitud de la respuesta de frecuencia se produce si cualquiera de los siguientes valores pasa cerca o sobre un cero, y en horas pico respuesta de magnitud ocurre si cualquiera de los siguientes valores pasa cerca de un poste:

El sistema no puede ser estable si un polo está en cualquiera de los valores.

Convolución con funciones de impulso

Cuando convolve cualquier cosa con

se obtiene el mismo nada a cambio, pero está desplazada t₀ o n₀. Caso en punto:

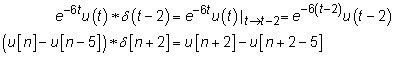
Spectrum en DC

La corriente directa (DC), o valor medio, de la señal de X(t) Impacta en el espectro de frecuencia correspondiente X(F) a F = 0. En el dominio de tiempo discreto, el mismo resultado se mantiene para la secuencia X[n], Excepto la periodicidad de

en el dominio de tiempo discreto que hace que el componente de DC en

Muestras de frecuencia de N puntos DFT

Si usted muestrea una señal de tiempo continuo X(t) En la tasa de F_s muestras por segundo para producir X[n] = X(n/F_s), Entonces usted puede cargar N muestras de X[n] En un Fourier de tiempo discreto transformada (DFT) - o una transformada rápida de Fourier (FFT), para lo cual N es una potencia de 2. Puntos de la DFT k corresponden a estos valores de frecuencia de tiempo continuo:

Asumiendo que X(t) Es una señal real, los puntos de DFT útiles van desde 0 a N/ 2.

Integrator y acumulador inestable

El integrador del sistema H_yo(s) = 1 /s y el sistema de acumuladores H_acc(z) = 1 / (1 - z^-1) Son inestables por sí mismos. ¿Por qué? Un polo en s = 0 o un poste en z = 1 no es bueno. Pero usted puede utilizar ambos sistemas para crear un sistema estable, colocándolos en una configuración de retroalimentación. Esta figura muestra los sistemas estables construidas con los bloques integradores y construcción acumulador.

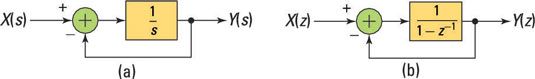
Puede encontrar las funciones del sistema de circuito cerrado estables por hacer el álgebra:

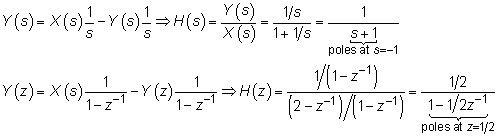
El espectro de un impulso rectangular

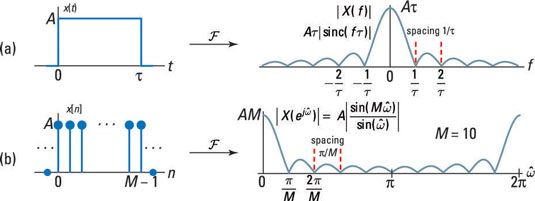
El espectro de una señal rectangular de pulso o la secuencia (que es la respuesta de frecuencia si ve la señal como la respuesta al impulso de un sistema LTI) tiene nulos espectrales periódicas. La relación de las señales continuas y discretas se muestra aquí.

Odd simetría de media onda y armónicos de la serie de Fourier

Una señal periódica con extraña simetría de media onda,

es el período, tiene representación en serie de Fourier consiste en armónicos única impares. Si, por alguna constante LA, y(t) = LA + X(t), Entonces la misma propiedad se mantiene con la adición de una línea de espectros a F = 0 (DC). Las olas y triángulo cuadrados formas de onda son tanto extraña simetría de media onda dentro de compensar una constante.