Realización de una transformada rápida de Fourier (FFT) en un archivo de sonido
Análisis de los datos toma muchas formas. A veces, es necesario buscar patrones en los datos de una manera que no podría haber considerado inicialmente. Una forma común para llevar a cabo tal análisis es utilizar una Transformada Rápida de Fourier (FFT) para convertir el sonido desde el dominio de la frecuencia al dominio del tiempo. Hacer esto le permite trazar el sonido de una manera nueva.
Por ejemplo, piense en un mecánico que toma una muestra de sonido de un motor y luego se basa en una máquina para analizar esa muestra, en busca de posibles problemas de motor. El diagnóstico puede encontrar algunos problemas y la inspección visual puede encontrar a otros, pero a veces el sonido de un motor revela problemas que usted no puede encontrar en ninguna otra manera.
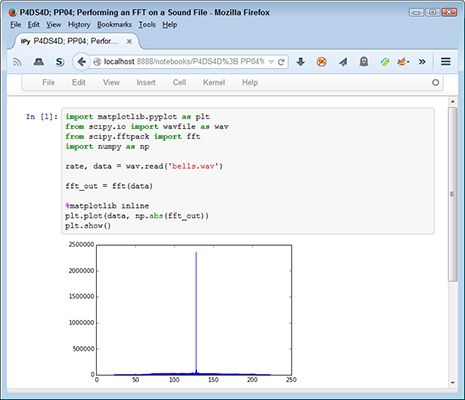
Aquí está el código que se utiliza para realizar una FFT:
matplotlib.pyplot importación como pltfrom scipy.io wavfile importación como wavfrom scipy.fftpack fftimport importación numpy como nprate, data = wav.read ('bells.wav') fft_out = fft (datos)% matplotlib inlineplt.plot (datos, np. abs (fft_out)) plt.show ()En este caso, se empieza por leer en el archivo de sonido y extraer el datos de eso. los tarifa información no es importante, ya que no es necesario saber qué tan rápido para reproducir los datos, sólo hay que saber qué valores contiene el sonido. Los valores de sonido consisten en frecuencia (el tono del sonido) y amplitud (qué tan fuerte para jugar).
El siguiente paso es realizar la FFT llamando fft () con datos. Este análisis particular es una simplificación de un proceso mucho más amplio. El punto es que la salida muestra las frecuencias más fuertes detectados a través del tiempo.
-
En caso de añadir sonido a tus infografía? - Juega con el sonido y el vídeo durante la grabación de podcasts con GarageBand de mac
-
Cómo insertar un objeto de sonido en las diapositivas de PowerPoint 2007 -
Cómo reproducir un sonido largo de varias diapositivas de PowerPoint 2007 - Iniciar, pausar y reanudar un archivo de sonido en una presentación de PowerPoint 2007
-
Cómo agregar un sonido desde el sitio Web de Microsoft para la diapositiva de PowerPoint
Cómo reproducir el sonido una vez transcurridos unos segundos en powerpoint 2007 Además de tocar el sonido automáticamente como una diapositiva de PowerPoint viene en pantalla o al hacer clic en el icono de sonido, se puede reproducir un sonido después de un momento o ha transcurrido dos. En otras palabras, usted puede hacer…
Cómo cambiar el tono de control de cuentas de usuario Windows 7 y Windows Vista preguntan si desea permitir o Cancelar casi cada intento de hacer algo en Windows. Se llama Control de cuentas de usuario (UAC) y es el intento de Microsoft para trinquete hasta la seguridad. Pero el sonido de los pitidos…
Programación de juegos HTML5: hacer ruido con el objeto de sonido Se utiliza el Sonar objeto de crear dos sonidos por objeto - un MP3 y un OGG - para asegurar que los efectos de sonido en el juego funcionará en la mayoría de los navegadores HTML5 compatibles.sndElement = new Sound (src)Crea un nuevo Sonar objeto…
Trabajando con audio en aplicaciones de iOS En concreto, hay dos maneras diferentes de iOS tiene para la aplicación de audio. Uno de ellos es una instancia de la AVAudioPlayer clase llamada, muy apropiadamente, un reproductor de audio-que ofrece la reproducción de datos de audio desde un…
Trazado de un archivo de sonido en ipython A veces es interesante ver cómo se ve un sonido. Al oír el sonido que dice una cosa al respecto, pero al ver que te dice otras cosas. Además, puede utilizar los datos de sonido como parte de un análisis.Por ejemplo, es posible que desee realizar…
Inserción de archivos de sonido en una diapositiva de PowerPoint Para reproducir el sonido en una presentación de PowerPoint 2007, se inserta un archivo de sonido en una diapositiva. ¿Cómo y cuándo se escucha el sonido depende de usted. Puede hacer que el archivo de sonido se reproduce automáticamente cuando…
Cómo pronunciar sonidos difíciles en el idioma chino La lengua china tiene algunos sonidos distintos que son puede ser difícil de pronunciar. Debe entenderse en chino, lo que necesita saber cómo se pronuncia estos sonidos, que tienden a dar a los angloparlantes algunos problemas. Una vez que el…
Elegir si desea utilizar el sonido en sus páginas web Muchas personas quieren tener una banda sonora o música ambiental en sus sitios Web. Los sonidos pueden hacer usando el sitio más agradable y contribuir a su personalidad. Idealmente, el usuario sería capaz de convertir fácilmente el sonido en…
Cómo añadir sonido a su página con coffeecup Aunque no es necesariamente una buena idea añadir sonido a su página Web, CoffeeCup hace un trabajo excelente de apoyar la incorporación de sonidos. Siga estos pasos para añadir sonido a una página Web en CoffeeCup:El usuario puede detener el…
¿Puedo obtener el sonido analógico con mi grabadora digital? Una tendencia interesante en la grabación de hogar digital es la búsqueda de sonido analógico. En el mercado, a encontrar nuevas piezas de equipo que se comercializan como tener calor o una sonido vintage. ¿Qué es exactamente este sonido?Este…
Conceptos básicos de grabación Inicio: canales midi Canales MIDI le permiten designar los mensajes que ir a una máquina en particular. Usted puede programar cada máquina para recibir mensajes en uno o más de los 16 canales MIDI. Por ejemplo, usted puede configurar su caja de ritmos para recibir…
Conceptos básicos de grabación Inicio: Los mensajes MIDI Para los instrumentos MIDI para comunicarse entre sí, tienen que tener un vocabulario común. Aquí es donde los mensajes MIDI vienen en mensajes MIDI contienen un conjunto de comandos, incluyendo las siguientes.:Mensajes de datos de rendimiento:…