Señales del mundo real y los sistemas de caso: resolver el problema de caída zoh dac en el dominio z

El orden cero de retención (ZOH), que es inherente a muchas de digital a analógico (DAC convertidores), mantiene la constante salida analógica entre muestras. La acción de los introduce ZOH freQuencaída cy, un rollo fuera de la respuesta de frecuencia efectiva DAC en el intervalo de frecuencia cero a la mitad de la frecuencia de muestreo F_s, en la reconstrucción y(t) de y[n]. Dos respuestas posibles son

• Aplicar un filtro de conformación función sinc inversa en el dominio de tiempo continuo.

• Correcta para la caída antes de la señal surge de la DAC.

El diagrama de bloques del sistema se muestra aquí.

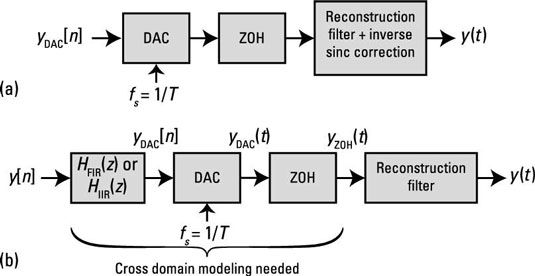
Imagine que un ingeniero jefe le pide que investigue la eficacia de la sencilla respuesta de impulso infinito (IIR) y la respuesta al impulso finita (FIR) Filtros digitales como una forma de mitigar ZOH caída de frecuencia. Tiene que comprobar lo bien que estos filtros funcionan realmente. Las funciones del sistema de filtro son

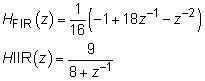
Para resolver este problema, es necesario utilizar la relación de dominio de frecuencia de la discrete- a los dominios de tiempo continuo. La relación, en relación con la notación de la figura, es

Se puede suponer que el filtro de reconstrucción analógica elimina espectros de señal más allá F_s/ 2.

La respuesta de frecuencia de interés resulta ser la cascada de

Siga estos pasos para justificar este resultado:

1. Dejar

   

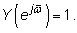
   Desde el teorema de convolución para espectros de frecuencia en el dominio de tiempo discreto, obtener

   

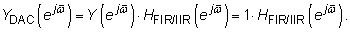
2. Utilice la relación discreta para espectros continuos para descubrir que el lado de salida del DAC es

   

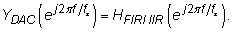
3. Utilice el teorema de convolución para espectros de frecuencia en el dominio de tiempo continuo para empujar los espectros de salida del DAC a través del filtro ZOH:

   

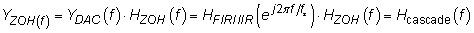
   El resultado de cascada se ha establecido.

Para ver la respuesta de frecuencia equivalente para este problema en el dominio de tiempo discreto, sólo tiene que cambiar las variables de acuerdo con la teoría del muestreo:

Reorganización de las variables en el resultado cascada se ve desde la perspectiva de tiempo discreto dominio es

La respuesta de frecuencia es ZOH

Juntando las piezas y considerando únicamente la respuesta de magnitud revela esta ecuación:

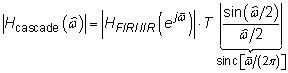
Para verificar el rendimiento, evaluar la función sinc y las respuestas FIR utilizando el SciPy signal.freqz () enfoque de la función de la receta dominio de la frecuencia. Echa un vistazo a los resultados en la siguiente figura.

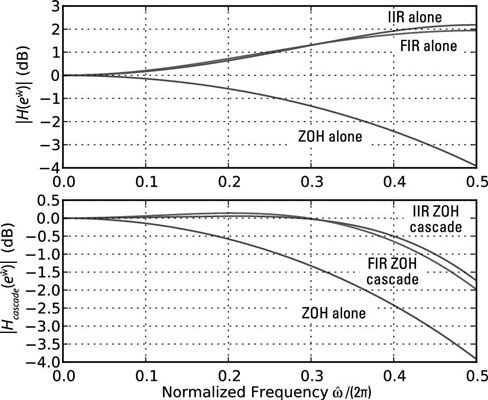
En [393]: W = linspace (0, pi, 400) En [394]: H_ZOH_T = sinc (w / (2 * pi)) En [395]: W, H_FIR = signal.freqz (array ([- 1, 18, -1]) / 16, 1, w) En [396]: W, H_IIR = signal.freqz ([- 9/8], [1, 1/8], w.). En [402]: Plot (w / (2 * pi), 20 * log10 (abs (H_ZOH_T))) En [403]: # Otras líneas cammand parcela similarIn [412]: Plot (w / (2 * pi), 20 * log10 (abs (H_FIR) * abs (H_ZOH_T)))

Estos resultados son bastante impresionantes para tales filtros de corrección simples. El objetivo es conseguir la llanura que está cerca de 0 dB de 0 a # 960- rad / muestra (0 a 0.5 normalizado). La respuesta es plana dentro de 0,5 dB a 0,4 rad / muestra para el IIR del Filtro es un poco peor para el filtro FIR.