Resolver integrales impropias con uno o dos límites infinitos de integración
Cuando integrales impropias tienen uno o dos límites infinitos de integración, puede resolver estas integrales, al convertirlos en los límites donde c tiende a infinito o infinito negativo. He aquí dos ejemplos:
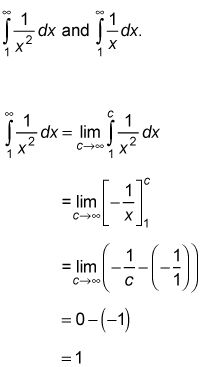
Así que esta integral impropia converge.
En la siguiente integral, el denominador es más pequeño, X en lugar de x2, y por lo tanto la fracción es más grande, por lo que se espera
que se encuentra. Pero no es sólo más grande, es camino más grande:
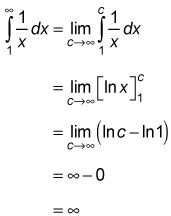
Esta integral impropia diverge.
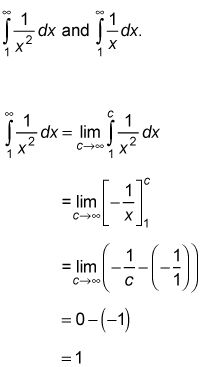
Esta figura muestra estas dos funciones: el área bajo
El área bajo
es exactamente el mismo que el área del cuadrado 1-a-1 a su izquierda: 1 unidad cuadrada. El área bajo
es mucho mucho más grande - de hecho, es infinitamente más grande que una lo suficientemente grande como plaza para encerrar la Vía Láctea. Sus formas son muy similares, pero sus áreas no podrían ser más diferentes.
Cuando ambos de los límites de integración son infinitos, dividir la integral en dos y encender cada parte en un límite. Dividir la integral en X = 0 es conveniente porque cero es un número fácil de tratar, pero se puede dividir en cualquier lugar que desee. Zero también puede parecer una buena opción, ya que parece que está en el medio entre
Pero eso es una ilusión, porque no hay medio entre
o se podría decir que cualquier punto de la X-eje es el medio.
He aquí un ejemplo:
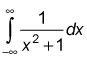
Dividir la integral en dos.
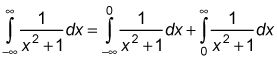
Gire cada parte en un límite.
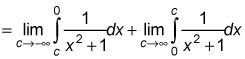
Evaluar cada parte y sumar los resultados.
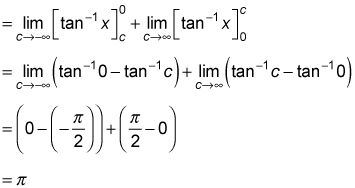
Es posible que desee hacer este problema de nuevo, dividiendo el alguna parte integrante que no sea en X = 0, para confirmar que se obtiene el mismo resultado.
Si bien "la mitad" integral diverge, el todo, integral diverge originales.
-
Comando Integral de TI-Nspire submenú cálculo cas -
Libro de Cálculo para dummies -
Calcular las integrales y representando integrales como funciones -
La determinación de si una serie converge utilizando la prueba de comparación integral -
La evaluación de las integrales dobles -
La evaluación de las integrales triples
Encuentra las zonas exactas bajo una curva mediante la integral definida Cuando se aproxima el área bajo una curva utilizando rectángulos, los más rectángulos que utiliza la izquierda, derecha, o punto medio, mejor será la aproximación. Por lo tanto, "todos" que tendría que hacer para conseguir el área exacta…
Encuentra el área bajo más de una función A veces, una sola área geométrica es descrito por más de una función. Por ejemplo, supongamos que desea encontrar el área sombreada que se muestra en la siguiente figura, el área bajo y = Sen X y y = Cos X de 0 a Pi-/ 2:La primera cosa a notar…
Encuentra la integral de funciones anidadas A veces es necesario integrar una función que es la composición de dos funciones - por ejemplo, la función 2X anidada dentro de una función seno. Si estaba diferenciando, se puede utilizar la regla de la cadena. Desafortunadamente, no existe una…
Cómo aproximar área con la regla trapezoidal Con la regla trapezoidal, en lugar de aproximar el área mediante el uso de rectángulos (como lo hace con la izquierda, derecha, y los métodos de rectángulo del punto medio), su área aproximada con - ¿puedes adivinar? - Trapezoides.Debido a la…
Cómo evaluar una integral impropia que es horizontalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA horizontalmente infinita integral impropia contiene ya sea # 8734- o - # 8734- (o ambos) como un límite de la integración.Evaluación de una integral impropia es un…
Cómo evaluar una integral impropia que es verticalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA verticalmente infinita integral impropia contiene al menos una asíntota vertical. Verticalmente integrales impropias infinitos son más difíciles de reconocer que los que…
¿Cómo encontrar zona con el método de sustitución u Puede utilizar el teorema fundamental para calcular el área debajo de una función (o simplemente para hacer cualquier edad integral definida) que se integran con el método de sustitución. Lo que quiero hacer es cambiar los límites de…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
¿Cómo resolver integrales impropias de funciones que tienen asíntotas verticales A resolver integrales impropias, al convertirlos en problemas de límite. No se puede hacer de ellos la manera regular. He aquí cómo resolver integrales impropias de funciones que tienen asíntotas verticales. Hay dos casos: una asíntota vertical…
¿Cómo resolver integrales impropias que tienen uno o dos límites infinitos de integración Una de las formas en que pueden ser integrales definidas inadecuada es cuando uno o ambos de los límites de integración son infinitas. A resolver este tipo de integral impropia al convertirlo en un problema de límite en c tiende a infinito o…
¿Cómo resolver los límites en el infinito con una calculadora Despejando límites en el infinito es fácil de hacer cuando se utiliza una calculadora. Por ejemplo, escribir la función debajo en el modo de gráficos de la calculadora:entonces ve a tpoder setup y establecer TblStart a 100.000 y # 8710-Tbl a…
Cómo dividir una integral definida en dos integrales definidas Cuando la solución de problemas de la zona, a veces es necesario dividir una integral en dos integrales definidas separadas. Aquí hay una regla simple, pero muy útil para hacer esto que parece complicado, pero es realmente muy fácil:Esta regla…