¿Cómo resolver integrales mediante la integración por partes

Usted puede pensar en la integración por partes como la versión de la integración de la regla del producto para la diferenciación. La idea básica de la integración por partes es transformar una integral que poder't hacerlo en un producto simple, menos un integrante que poder hacer. Aquí está la fórmula:

Integración por la fórmula partes:

Y aquí está una ayuda de memoria para ello: En los primeros dos trozos,

el u y v están en orden alfabético. Si te acuerdas de eso, se puede recordar que la integral de la derecha es igual que el de la izquierda, excepto el u y v se invierten.

No trates de entender la fórmula todavía. Vas a ver cómo funciona en un minuto. Y no se preocupe por entender el primer ejemplo, hasta llegar a la final de la misma. La integración por partes proceso puede parecer bastante enrevesado la primera vez que a través de él, así que tienes que ser paciente. Después de trabajar a través de un par de ejemplos, verás que en realidad no es tan malo en absoluto.

La integración por partes la caja: La integración por la fórmula partes contiene cuatro cosas: u, v, du, y dv. Para ayudar a mantener todo recto, a organizar sus problemas con un cuadro como el que se muestra aquí.

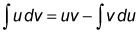
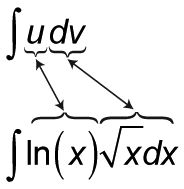
Para el primer ejemplo, trate

La integración por la fórmula partes convertirá esta integral, que no se puede hacer directamente, en un simple producto, menos una integral usted sabrá cómo hacerlo. En primer lugar, tienes que dividir el integrando en dos trozos - un solo trozo se convierte en el u y el otro el dv que se ve en el lado izquierdo de la fórmula. Para este problema, los ln (X) Se convertirá en su u trozo. Entonces todo lo demás es la dv trozo, a saber,

Después de volver a escribir el integrando más arriba, usted tiene el siguiente para el lado izquierdo de la fórmula:

Ahora es el momento de hacer la cosa caja. Para cada nuevo problema, se debe dibujar un cuadro de cuatro plaza vacía, entonces pone su u (ln (X) En este problema) en la plaza superior izquierda y su

en la plaza inferior derecha, como se muestra en la siguiente figura.

A continuación, a diferenciar u para obtener su du, y se integra dv para obtener su v. Las flechas en la segunda figura recuerdan a diferenciar a la izquierda y para integrar a la derecha. Piense en la diferenciación - la cosa más fácil - como ir hacia abajo (como ir cuesta abajo), y la integración - la cosa más difícil - como subir (como ir cuesta arriba).

Ahora completar el cuadro:

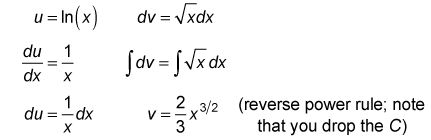
El cuadro completo para

se muestra en la siguiente figura.

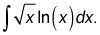
También puede utilizar el cuadro de cuatro cuadrados para ayudarle a recordar el lado derecho de la fórmula de integración por partes: comienza en la plaza superior izquierda y dibujar (o cuadro apenas) un número de 7 va en línea recta hacia la derecha, a continuación, en diagonal hacia abajo a la izquierda, como se muestra en la siguiente figura.

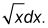
Recordando cómo se "dibuja" el 7, mira de nuevo a la figura anterior. El lado derecho de la fórmula de integración por partes te dice que hacer la parte superior de la 7, a saber,

menos la integral de la parte diagonal de la 7,

Por cierto, todo esto es mucho fácil de hacer que de explicar. Intentalo. Verás cómo este esquema de cuatro cuadrados cuadro le ayuda a aprender la fórmula y organizar estos problemas.

Listo para terminar? Conecte todo en la fórmula:

En el último paso, se sustituye el # 8201;

veces cualquier número vieja sigue siendo sólo un número viejo.