Determinar el área entre las curvas sin signo
Usted puede utilizar el concepto de área sin firmar para medir el área entre las curvas. Por ejemplo, puede utilizar esta técnica para encontrar la zona de sombra sin firmar en la siguiente figura.
En este ejemplo, va a aproximar su respuesta a dos decimales utilizando
El primer paso es encontrar una ecuación para la solución (que probablemente le dará crédito parcial), y luego preocuparse por resolverlo.
En primer lugar, dividir el área sombreada en tres regiones etiquetados A, B y C. También debe etiquetar región D, que debe tener en cuenta. Darse cuenta de X = separa las regiones A y B, y el X-eje separa las regiones B y C.
Usted puede encontrar tres ecuaciones independientes para las regiones A, B, y C, pero no hay una mejor manera.
Para medir el área sin firmar entre dos funciones, utilice este truco rápido:
Área = Integral de Top Función - Integral de la Función Inferior
¡Eso es! En lugar de medir la zona superior y por debajo del X-eje, sólo tiene que enchufar los dos integrales en esta fórmula. En este problema, la función de la parte superior es de 4X - X2 y la función fundamental es el pecado X:
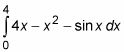
Esta evaluación no es demasiado horrible:
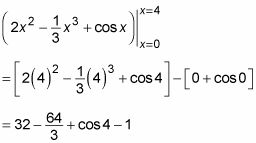
Al llegar a este punto, ya se puede ver que estás en el buen camino, porque el profesor era lo suficientemente bueno para darle un valor aproximado para cos 4:
Así que el área sin signo entre las dos funciones es de aproximadamente 9,02 unidades.
Si las dos funciones cambian posiciones - es decir, la parte superior se convierte en la parte inferior y la parte inferior se convierte en la parte superior - puede que tenga que romper el problema en regiones. Pero incluso en este caso, todavía se puede ahorrar mucho tiempo utilizando este truco.
He aquí otro ejemplo: Encuentra el área entre y = X y
como se muestra en esta figura.
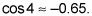
En primer lugar, medir el área sombreada de la figura por medio de cuatro regiones separadas. He aquí cómo hacerlo utilizando el truco de arriba y abajo.
Observe que las dos funciones se cruzan en X = 1. Entonces, de 0 a 1, la función superior es
y de 1 a 2, la función de la parte superior es X. Así que la creación de dos ecuaciones separadas, una para la región A y otra para la región B:
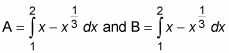
Cuando los cálculos están completos, se obtienen los siguientes valores para A y B:
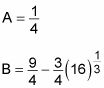
Añadir estos dos valores para obtener su respuesta:
Como se puede ver, el truco de arriba y abajo le consigue la misma respuesta mucho más simple que las regiones de medición.
Encontrar el área de una superficie de revolución Lo bueno de hallar el área de una superficie de revolución es que no hay una fórmula que puede utilizar. Memorizarlo y ya está a medio camino hecho.Para encontrar el área de una superficie de revolución entre la y b, utilizar la siguiente…
Encuentra el área bajo más de una función A veces, una sola área geométrica es descrito por más de una función. Por ejemplo, supongamos que desea encontrar el área sombreada que se muestra en la siguiente figura, el área bajo y = Sen X y y = Cos X de 0 a Pi-/ 2:La primera cosa a notar…
Encuentra el área entre dos funciones Para encontrar un área entre dos funciones, es necesario establecer una ecuación con una combinación de integrales definidas de ambas funciones. Por ejemplo, suponga que desea calcular el área sombreada entre y = X2 ycomo se muestra en esta…
Cómo aproximar el área del punto medio con rectángulos Una buena manera de aproximarse a las zonas con rectángulos es hacer que cada rectángulo cruzar la curva en el punto medio de la parte superior de ese rectángulo. Una suma punto medio es una mejor estimación del área que cualquiera a la…
Cómo evaluar una integral impropia que es verticalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA verticalmente infinita integral impropia contiene al menos una asíntota vertical. Verticalmente integrales impropias infinitos son más difíciles de reconocer que los que…
¿Cómo encontrar el área con la versión de acceso directo del teorema fundamental del cálculo El teorema fundamental del cálculo tiene una versión de acceso directo que hace que encontrar el área bajo una curva en un instante. Aquí está. Dejar F ser cualquier antiderivada de la función F- despuésCon esta versión del teorema…
¿Cómo encontrar el área entre dos curvas Para encontrar el área entre dos curvas, lo que necesita para llegar a una expresión para un rectángulo estrecho que se encuentra en una curva y sube a otro.de X = 0 a X = 1:Para obtener la altura del rectángulo de representación en la figura,…
Cómo dividir una integral definida en dos integrales definidas Cuando la solución de problemas de la zona, a veces es necesario dividir una integral en dos integrales definidas separadas. Aquí hay una regla simple, pero muy útil para hacer esto que parece complicado, pero es realmente muy fácil:Esta regla…
Calcular rápidamente integrales definidas utilizando el teorema fundamental Este es un teorema de integración atajo requete que utilizará para el resto de tus días naturales nacidos - o por lo menos hasta el final de su temporada con el cálculo. Este método de acceso directo es todo lo que necesita para la mayoría de…
El teorema fundamental del cálculo El teorema fundamental del cálculo es uno de los teoremas más importantes en la historia de las matemáticas. Establece que, dada una función de área LAF que barre área bajo F (t),la velocidad a la que el área está siendo barrido es igual a…
Determinar el área de un triángulo desde su base y la altura Si conoce la base y la altura de un triángulo, puede utilizar una fórmula probada y verdadera para encontrar su área. Es probable que primero encontró con la fórmula básica área del triángulo en aproximadamente sexto o séptimo grado. Si ha…
Cómo determinar el área de sectores y segmentos de un círculo Marque una sección de un círculo con un arco y una cuerda, y usted tiene un segmento (este tipo de segmento tiene nada que ver con un segmento de línea). Lanzar un par de radios alrededor de un arco, y usted tiene un sector.Así que aquí están…