¿Cómo encontrar el área de una superficie de revolución
Una superficie de revolución es una superficie en tres dimensiones con secciones transversales circulares, como un florero o una campana o una botella de vino. Para estos problemas, se divide la superficie en bandas circulares estrechos, calcular el área superficial de una banda representativa, y luego simplemente suman las áreas de todas las bandas para obtener la superficie total. La siguiente figura muestra una forma tal con una banda representativa.
¿Cuál es la superficie de una banda representativa? Bueno, si se corta la banda y desenrolla, se obtiene una especie de largo, estrecho rectángulo cuya área, por supuesto, es largo veces ancho.
Superficie de Revolución: Una superficie generado al girar una función, y = F (X), Alrededor de un eje tiene un área de superficie - entre la y b - dado por la siguiente integral:
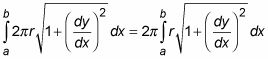
Por cierto, en la explicación anterior, puede que se pregunte por qué el ancho de la banda rectangular es
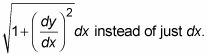
Es porque el poco ancho de banda está inclinada en lugar de horizontal (en cuyo caso sería sólo dx). El hecho de que está inclinado hace que funcione como la hipotenusa de un triángulo rectángulo pequeño. La expresión de fantasía de futuro para el ancho de la banda proviene de la elaboración de la longitud de esta hipotenusa con el Teorema de Pitágoras. Eso debería hacer que se sienta mucho mejor!
Si el eje de revolución es el X-eje, r será igual F (X) - Como se muestra en la figura anterior. Si el eje de revolución alguna otra línea, como y = 5, que es un poco más complicado - algo que esperamos con interés.
Ahora trata de un problema: ¿Cuál es el área de superficie - entre X = 1 y X = 2 - de la superficie generada al girar
acerca de X-eje?
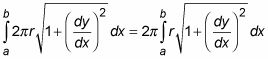
Tome la derivada de su función.
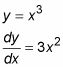
Ahora usted puede terminar el problema con sólo enchufar todo en la fórmula, pero debes hacerlo paso a paso para reforzar la idea de que cada vez que se integran, de anotar un poco representativa de algo - que es el integrando - a continuación, se suman todos los pequeños trozos de integración.
Calcule el área de superficie de una banda estrecha representativa.
Sume las áreas de todas las bandas de 1 a 2 mediante la integración.
¿Cómo encontrar el área de volumen y superficie del cuerno de gabriel Encontrar el área de volumen y superficie de este problema bocina puede volar tu mente. Cuerno de Gabriel es el sólido generado al girar sobre el X-eje de la región sin límites entreEsta cifra muestra un gráfico del cuerno de Gabriel.Jugar este…
¿Cómo encontrar el volumen de un sólido entre dos superficies de revolución Si desea encontrar el volumen de un sólido que se encuentra entre dos superficies distintas de la revolución, puede utilizar el método de carne máquina de cortar para hacer esto. los Método de carne máquina de cortar funciona mejor con los…
La medición de volumen bajo una superficie usando una integral doble Una integral doble le permite medir el volumen bajo una superficie tan limitada por un rectángulo. Integrales definidas proporcionan una forma confiable de medir el área firmado entre una función y la X-eje como limitada por cualquiera de los dos…
Solución de problemas de integración en el cálculo Cálculo acertijo: ¿Qué teorema del valor medio, la lavadora y Métodos de Shell, y la longitud del arco y de la superficie de las fórmulas de la revolución tienen en común? Todos ellos implican la integración. La integración es además muy…
La determinación de la superficie de un triángulo equilátero Para calcular el área de un triángulo - para la mayoría de tipos de triángulos - lo que necesita saber de base y la altura del triángulo. Sin embargo, con un triángulo equilátero, todo lo que necesitas saber es la longitud de uno de sus…
Cómo averiguar el área de preguntas de la prueba de aritmética Una definición muy suelto de área es "la cantidad de cosas que podría caber en el suelo». Dependiendo de cómo la forma grande que estamos viendo es decir, medir el área en centímetros cuadrados (cm2), Metros cuadrados (m2) O…
Cómo nanotecnología maximiza el área de superficie La diminuta naturaleza de nanopartículas resultados en algunas características útiles, tales como una mayor superficie a la que otros materiales puede unir en formas que hacen de materiales ligeros más fuertes o más. En la nanoescala, el…
Fórmulas de geometría famosos que usted debe saber para el ASVAB Las subpruebas de matemáticas del ASVAB menudo piden que utilizar fórmulas básicas de geometría para calcular mediciones geométricas. Usted debe comprometerse estas fórmulas simples para la memoria si usted está esperando para una puntuación…
¿Cómo resolver problemas geométricos en el ASVAB Problemas geométricos en el ASVAB requieren que calcular el volumen, perímetro, área, circunferencia, diámetro, y así sucesivamente de varias formas geométricas. Estos problemas no son muy difíciles con un poco de conocimiento de algunas…
Calculadoras pisos Diy Hacer bricolaje sencilla de solado con un poco de planificación. Cuando estás poniendo un piso a ti mismo, averiguar cuántas baldosas o la cantidad de alfombra que necesita con estos cálculos a mano (si usted elige para medir en metros y…
¿Cuánto baldosas de cerámica se puede pedir? Si su plan de mejoras para el hogar implica un nuevo piso de baldosas de cerámica, ¿cómo se determina la cantidad de baldosas cerámicas que necesita? Simplemente calcular el área que va a cubrir y dividir ese número por el tamaño de una…
¿Cuánto pisos de vinilo se puede pedir? ¿Su proyecto de mejoras para el hogar implica un nuevo piso de vinilo? Para averiguar cuántas baldosas de vinilo, o lámina de vinilo, es necesario, siga estas fórmulas simples:Vinilo calculadora baldosaPara averiguar cuántas baldosas de vinilo…