Tasas relacionadas: el canal de problema de comida para cerdos
Digamos que usted está llenando su piscina y usted sabe cómo el agua rápido está saliendo de su manguera, y desea calcular qué tan rápido el nivel de agua de la piscina está en aumento. Usted conoce uno tasa (qué tan rápido se está vertiendo en el agua), y desea determinar otra velocidad (lo rápido que el nivel de agua está aumentando). Estas tarifas son llamadas tasas relacionados porque uno depende del otro - el más rápido el agua se vierte en el más rápido del nivel del agua subirá. En un típico problema de las tasas correspondientes, el tipo o tipos que te dan son inmutables, pero el precio que tiene que averiguar está cambiando con el tiempo. Usted tiene que determinar esta tasa en un punto determinado en el tiempo.
Aquí hay un problema tasas relacionadas jardín-variedad. Un canal se llena con comida para cerdos. Es de 10 pies de largo, y su sección transversal es un triángulo isósceles que tiene una base de 2 pies y una altura de 2 pies y 6 pulgadas (con el vértice en la parte inferior, por supuesto). El ser de Swill vierte a un ritmo de 5 pies cúbicos por minuto. Cuando la profundidad de la comida para cerdos es de 1 pie 3 pulgadas, la rapidez es el nivel de las aguas grasas aumento?
Dibuje un diagrama, etiquetando el diagrama con cualquier inmutable mediciones y variables asignar a cualquier cambiar cosas.
Es importante que tu figura muestra la inmutable Dimensiones de la cubeta - 2 pies, 2 pies 6 pulgadas y 10 pies - y que usted no da estas dimensiones nombres de variables como l de longitud o h para la altura. Y tenga en cuenta que la cambiar cosas - la altura (o profundidad) de la bazofia y la anchura de la superficie de la comida para cerdos (que se ensancha mientras que los desperdicios se hace más profunda) - deben tener nombres de variables, como h de altura y b para la base. (Se llama la base en vez de ancho porque es la base de la forma de triángulo al revés hecha por la comida para cerdos.) El volumen de los desperdicios también está cambiando, así que usted puede llamar a eso V, Claro.
Lista de todos los tipos dados y la tasa se le pedirá que averiguar como derivados con respecto a hora.
Escriba la fórmula que conecta las variables del problema: V, h, y b.
La fórmula para el volumen de un prisma recto (la forma de la comida para cerdos en el canal) es
V = (área de la base) (altura)
Esta "base" es la base del prisma (todo el triángulo en el extremo de la cubeta), no la base del triángulo, que está etiquetado b en la figura. Además, esta "altura" es la altura del prisma (la longitud de la cubeta), no la altura h marcado en la figura.
El área de la base triangular es igual
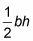
y la "altura" del prisma es de 10 pies, por lo que la fórmula se convierte en
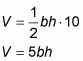
Encuentra una ecuación que relaciona la variable no deseado, b, a alguna otra variable en el problema para que pueda hacer un cambio para que te deja con solamente V y h.
La cara triangular de la comida para cerdos en el canal es similar a la cara triangular del propio comedero, por lo que la base y la altura de estos triángulos son proporcionales. Por lo tanto,
Tenga en cuenta que los triángulos semejantes surgen un montón de problemas relacionados con las tasas. Mira para ellos cada vez que el problema implica un triángulo, un prisma triangular, o una forma de cono.
Ahora sustituir 0.8h para b en su fórmula desde el paso 3.
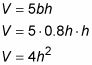
Diferenciar esta ecuación con respecto a t.
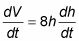
Sustituye los valores conocidos de la tasa y la variable en la ecuación del Paso 5 y luego resolver.
Eso es. Nivel de la comida para cerdos está aumentando a un ritmo de 2.1 pie por minuto cuando la comida para cerdos es de 1 pie 3 pulgadas de profundidad. ¡Cavar en!
Encontrar el volumen de un sólido con secciones transversales congruentes Saber cómo se mide el volumen sin cálculo da sus frutos a lo grande cuando entras en la arena cálculo. Esto es estrictamente obviedad cosas - algunos geometría básica y sólida que usted probablemente ya sabe.Uno de los sólidos más simples…
Cómo hacer un problema relacionado tasa implica una pelota de béisbol en movimiento Usted puede usar el cálculo para determinar una tasa que está relacionado con la velocidad de un objeto en movimiento. Por ejemplo, digamos que un pitcher lance una bola rápida, que el bateador emergente - que va hacia arriba por encima del…
¿Cómo encontrar el cambio de distancia entre dos objetos móviles En un típico problema de las tasas relacionadas, por ejemplo, cuando usted está encontrando un cambio en la distancia entre dos objetos en movimiento, la tasa o tasas de la información dada es constante, inmutable, y usted tiene que encontrar una…
Cómo medir el volumen de un sólido de forma irregular Se puede medir el volumen de cualquier sólido con una sección transversal que es una función de de forma irregular X. En algunos casos, estos sólidos son más difíciles de describir de lo que son para medir. Por ejemplo, echar un vistazo a esta…
Tasas relacionadas: dos vehículos en un cruce de caminos Digamos que usted está llenando su piscina y usted sabe cómo el agua rápido está saliendo de su manguera, y desea calcular qué tan rápido el nivel de agua de la piscina está en aumento. Usted conoce uno tasa (qué tan rápido se está…
Tasas relacionadas: el problema del globo en expansión Digamos que usted está llenando su piscina y usted sabe cómo el agua rápido está saliendo de su manguera, y desea calcular qué tan rápido el nivel de agua de la piscina está en aumento. Usted conoce uno tasa (qué tan rápido se está…
Determinar el área de un triángulo desde su base y la altura Si conoce la base y la altura de un triángulo, puede utilizar una fórmula probada y verdadera para encontrar su área. Es probable que primero encontró con la fórmula básica área del triángulo en aproximadamente sexto o séptimo grado. Si ha…
La determinación de la superficie de un triángulo equilátero Para calcular el área de un triángulo - para la mayoría de tipos de triángulos - lo que necesita saber de base y la altura del triángulo. Sin embargo, con un triángulo equilátero, todo lo que necesitas saber es la longitud de uno de sus…
Encontrar la altitud de un triángulo La altitud de un triángulo es un segmento de un vértice del triángulo hacia el lado opuesto (o a la extensión del lado opuesto si es necesario) que es perpendicular a la opuesta lateral del lado opuesto se llama la base. (Se utiliza la…
Cómo calcular el área de un paralelogramo, cometa, o trapezoidal Las fórmulas del área para el paralelogramo, cometa, y trapezoide se basan en el área de un rectángulo. Las siguientes figuras muestran cómo cada uno de estos tres cuadriláteros se refiere a un rectángulo, y la siguiente lista te da los…
Cómo determinar la distancia al horizonte Incluso antes de que Colón navegó a través del Océano Atlántico (tanto " demostrando " la tierra era redonda), los matemáticos ya había desarrollado una fórmula muy sencilla para calcular la distancia hasta el horizonte. Aunque muchas de las…
Cómo usar la trigonometría para encontrar el área de un triángulo A veces, la búsqueda de una medida que no es tan fácil. Puede que tenga que hacer frente a una forma irregular, como un triángulo, o incluso calcular su camino alrededor de un objeto fijo. En cualquier caso, puede utilizar la trigonometría para…