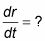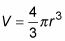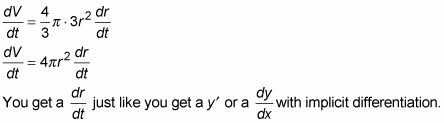Tasas relacionadas: el problema del globo en expansión
Digamos que usted está llenando su piscina y usted sabe cómo el agua rápido está saliendo de su manguera, y desea calcular qué tan rápido el nivel de agua de la piscina está en aumento. Usted conoce uno tasa (qué tan rápido se está vertiendo en el agua), y desea determinar otra velocidad (lo rápido que el nivel de agua está aumentando). Estas tarifas son llamadas tasas relacionados porque uno depende del otro - el más rápido el agua se vierte en el más rápido del nivel del agua subirá. En un típico problema de las tasas correspondientes, el tipo o tipos que te dan son inmutables, pero el precio que tiene que averiguar está cambiando con el tiempo. Usted tiene que determinar esta tasa en un punto determinado en el tiempo.
Por ejemplo, digamos que usted está inflando un globo a una velocidad de 300 pulgadas cúbicas por minuto. Cuando el radio del globo es de 3 pulgadas, qué tan rápido está aumentando el radio?

Dibuja un diagrama de etiquetar el diagrama con cualquier inmutable mediciones (no hay ninguno en esta inusualmente sencilla problema) y asegúrese de asignar una variable a nada en el problema de que es cambiar (a menos que, por supuesto, es irrelevante para el problema).
El radio en la figura se marca con la variable r. El radio necesita una variable ya que, como el globo está siendo volado, el radio es cambiar. En la figura, 3 es de paréntesis, a destacar que el número 3 es no una medida que no cambia. El problema pide a determinar algo cuando el radio es de 3 pulgadas, pero recuerda, el radio está en constante cambio.
En los problemas de las tasas correspondientes, es importante distinguir entre lo que está cambiando y lo que es no cambiante.
El volumen del globo también está cambiando, por lo que necesita una variable para el volumen, V. Se puede poner un V en su diagrama para indicar el volumen de cambio, pero no hay realmente ninguna manera fácil de etiquetar parte del globo con una V como se puede mostrar el radio con un r.
Lista de todos los tipos dados y la tasa se te pide para determinar como derivados con respecto al tiempo.
Usted está inflando el globo a 300 cubic pulgadas por minuto. Esa es una tasa de - es un cambio en el volumen (pulgadas cúbicas) por el cambio en el tiempo (minutos). Por lo tanto,

Usted tiene que averiguar qué tan rápido el radio está cambiando, por lo que
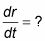
Escriba la fórmula que conecta las variables en el problema, V y r.
Ésta es la fórmula para el volumen de una esfera:
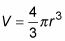
Diferenciar su fórmula con respecto al tiempo, t.
Esto funciona como la diferenciación implícita porque estás diferenciador con respecto a t, pero la fórmula se basa en algo más, a saber, r.
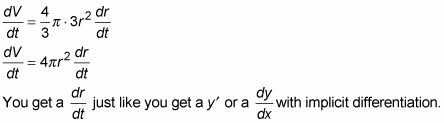
Sustituye los valores conocidos para la tasa y las variables en la ecuación del paso 4, y luego resolver la cosa se le pedirá que determine.

Asegúrese de diferenciar (Paso 4) antes de conectar la información dada en las incógnitas (paso 5).

Así, el radio está aumentando a un ritmo de aproximadamente 2,65 pulgadas por minuto cuando el radio mide 3 pulgadas. Piensa en todos los globos que ha volado desde su infancia. Ahora que por fin tiene la respuesta a la pregunta que te ha estado molestando durante todos estos años.
Por cierto, si se conecta en 5 r, en lugar de 3, se obtiene una respuesta de aproximadamente 0,95 pulgadas por minuto. Este hecho debe estar de acuerdo con su experiencia en globo de voladura - cuanto más grande es el globo consigue, más lentamente crece.
Sobre el autor
 Encontrar el volumen de un sólido utilizando el método de disco
Encontrar el volumen de un sólido utilizando el método de disco Cuando las secciones transversales de un sólido son todos los círculos, se puede dividir la forma en discos para encontrar su volumen. Así es como funciona. Digamos que usted necesita para encontrar el volumen de un sólido - entre X = 2 y X = 3…
 Cómo hacer un problema relacionado tasa implica una pelota de béisbol en movimiento
Cómo hacer un problema relacionado tasa implica una pelota de béisbol en movimiento Usted puede usar el cálculo para determinar una tasa que está relacionado con la velocidad de un objeto en movimiento. Por ejemplo, digamos que un pitcher lance una bola rápida, que el bateador emergente - que va hacia arriba por encima del…
 ¿Cómo encontrar el cambio de distancia entre dos objetos móviles
¿Cómo encontrar el cambio de distancia entre dos objetos móviles En un típico problema de las tasas relacionadas, por ejemplo, cuando usted está encontrando un cambio en la distancia entre dos objetos en movimiento, la tasa o tasas de la información dada es constante, inmutable, y usted tiene que encontrar una…
 Cómo utilizar el método Shell para medir el volumen de un sólido
Cómo utilizar el método Shell para medir el volumen de un sólido los método de shell permite medir el volumen de un sólido mediante la medición del volumen de muchas superficies concéntricas de volumen, llamado " conchas ". Aunque el método de shell funciona sólo para sólidos con secciones transversales…
 Tasas relacionadas: el canal de problema de comida para cerdos
Tasas relacionadas: el canal de problema de comida para cerdos Digamos que usted está llenando su piscina y usted sabe cómo el agua rápido está saliendo de su manguera, y desea calcular qué tan rápido el nivel de agua de la piscina está en aumento. Usted conoce uno tasa (qué tan rápido se está…
 Tasas relacionadas: dos vehículos en un cruce de caminos
Tasas relacionadas: dos vehículos en un cruce de caminos Digamos que usted está llenando su piscina y usted sabe cómo el agua rápido está saliendo de su manguera, y desea calcular qué tan rápido el nivel de agua de la piscina está en aumento. Usted conoce uno tasa (qué tan rápido se está…
 Cómo comparar los tamaños de división en dos pizzas utilizando la trigonometría
Cómo comparar los tamaños de división en dos pizzas utilizando la trigonometría Algunos hermanos de la fraternidad quieren pedir una pizza - y usted sabe lo hambriento hombres universitarios pueden ser. La gran pregunta es, que tiene rebanadas grandes de la pizza: un corte de pizza de 12 pulgadas en seis rodajas, o una pizza de…
 Cómo determinar la altitud de un globo
Cómo determinar la altitud de un globo Puede utilizar las funciones trigonométricas para determinar la altitud de un globo. Cindy y Mindy, de pie a una milla de distancia, detectar un globo de aire caliente directamente sobre un punto determinado de la tierra en algún lugar entre…
 ¿Cómo se mide la velocidad de un coche alrededor de una pista de carreras
¿Cómo se mide la velocidad de un coche alrededor de una pista de carreras Un coche de carreras va alrededor de una pista circular. Un fotógrafo de pie en el centro de la pista toma una foto, se convierte de 80 grados, y luego toma otra foto 10 segundos después. Si la pista tiene un diámetro de 1.2 millas, lo rápido…
 Radio, diámetro, circunferencia, y el área de círculos
Radio, diámetro, circunferencia, y el área de círculos LA círculo es una figura geométrica que necesita sólo dos piezas que lo identifican y clasifican: su centro (o medio) y su radio (la distancia desde el centro hasta cualquier punto en el círculo). Después de elegir un punto para ser el centro…
 ¿Cómo resolver problemas geométricos en el ASVAB
¿Cómo resolver problemas geométricos en el ASVAB Problemas geométricos en el ASVAB requieren que calcular el volumen, perímetro, área, circunferencia, diámetro, y así sucesivamente de varias formas geométricas. Estos problemas no son muy difíciles con un poco de conocimiento de algunas…
 Preguntas de ejemplo de GED: aplicación real de las preguntas de razonamiento matemático
Preguntas de ejemplo de GED: aplicación real de las preguntas de razonamiento matemático La sección de Razonamiento Matemático del GED le hará preguntas que requieren que para aplicar las habilidades matemáticas a las aplicaciones de la vida real. Echa un vistazo a los siguientes ejemplos para ver lo que se puede encontrar el día…