¿Cómo encontrar el cambio de distancia entre dos objetos móviles

En un típico problema de las tasas relacionadas, por ejemplo, cuando usted está encontrando un cambio en la distancia entre dos objetos en movimiento, la tasa o tasas de la información dada es constante, inmutable, y usted tiene que encontrar una tasa relacionada que está cambiando con hora. Usted tiene que determinar esta tasa relacionada en un momento determinado en el tiempo.

He aquí un ejemplo: Un coche sale una intersección viajando hacia el norte a 50 mph, otra está conduciendo al oeste, hacia la intersección en 40 mph. En un momento, el coche con rumbo al norte es tres décimas de una milla al norte de la intersección, y el coche con rumbo al oeste es de cuatro décimas de milla al este de la misma. En este punto, la rapidez es la distancia entre los coches cambiantes?

1. Comience por crear un diagrama.

   
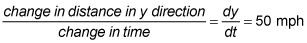   Cálculo - es una unidad en el país.

   Antes de continuar con este problema, considere un problema similar que puede correr a través de si usted está utilizando un libro de texto de cálculo estándar. Se trata de una escalera inclinada contra y arrastrando hacia abajo una pared. ¿Puedes ver que el diagrama para un problema tan escalera sería muy similar a esta figura, salvo que el y-eje representaría la pared, el X-eje sería el suelo, y la línea diagonal sería la escalera? Estos problemas son bastante similares, pero hay una diferencia importante. La distancia entre los coches es cambiar por lo que la línea diagonal en la figura se etiqueta con una variable, s. Una escalera, por otro lado, tiene una fijo de longitud, por lo que la línea diagonal en su diagrama para el problema de la escala se etiquetan con un número, no una variable.

2. Lista de todos los tipos dados y la tasa desconocida.

   Como Coche A viaja hacia el norte, la distancia y está creciendo a 50 millas por hora. Esa es una tasa, un cambio en la distancia por el cambio en el tiempo. Por lo tanto,

   

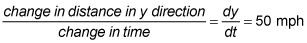
   Como coche B viaja al oeste, la distancia X es encogimiento a 40 millas por hora. Eso es un negativo tasa:

   

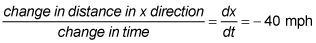
   Tienes que encontrar la manera rápida s es cambiante, por lo que,

   

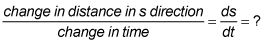
3. Escriba la fórmula que relaciona las variables del problema: X, y, y s.

   El teorema de Pitágoras, la² + b² = c², hará el truco para este problema triángulo rectángulo. En este problema, X y y son las patas del triángulo rectángulo, y s es la hipotenusa, por lo X² + y² = s².

   El teorema de Pitágoras se utiliza mucho en los problemas relacionados con las tasas. Si hay un triángulo rectángulo en su problema, es muy probable que la² + b² = c² es la fórmula que necesita.

   Debido a que esta fórmula contiene las variables x, y, y s que todos aparecen en la lista de los derivados en el paso 2, usted no tiene que modificar esta fórmula.

4. Diferenciar con respecto al t.

   

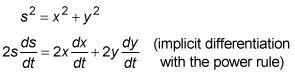
   (Recuerde, en un problema de tarifas relacionadas, todas las variables se tratan como el ys en un problema implícita diferenciación.)

5. Sustituir y resuelve para

   

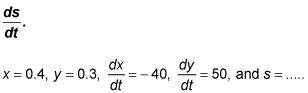
   "Distancia desprovisto Santo carente longitud, Batman. ¿Cómo se puede resolver

   

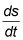
   ? a menos que tenga los valores para el resto de las incógnitas en la ecuación "" Tome un calmante, Robin - sólo tiene que utilizar el teorema de Pitágoras de nuevo. "

   

   Usted puede rechazar la respuesta negativa porque s obviamente, tiene una longitud positiva. Así s = 0,5.

   Ahora conecte todo en su ecuación:

   

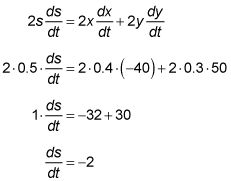
Esta respuesta negativa significa que la distancia, s, es decreciente.

Por lo tanto, cuando el coche A es 3 cuadras al norte de la intersección y el coche B está a 4 cuadras al este de la misma, la distancia entre ellos está disminuyendo a un ritmo de 2 mph.