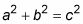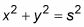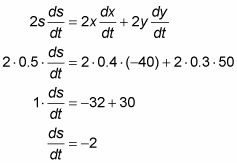Tasas relacionadas: dos vehículos en un cruce de caminos
Digamos que usted está llenando su piscina y usted sabe cómo el agua rápido está saliendo de su manguera, y desea calcular qué tan rápido el nivel de agua de la piscina está en aumento. Usted conoce uno tasa (qué tan rápido se está vertiendo en el agua), y desea determinar otra velocidad (lo rápido que el nivel de agua está aumentando). Estas tarifas son llamadas tasas relacionados porque uno depende del otro - el más rápido el agua se vierte en el más rápido del nivel del agua subirá. En un típico problema de las tasas correspondientes, el tipo o tipos que te dan son inmutables, pero el precio que tiene que averiguar está cambiando con el tiempo. Usted tiene que determinar esta tasa en un punto determinado en el tiempo.
En este ejemplo, un coche sale una intersección viajando hacia el norte a 50 mph, y otro está conduciendo al oeste, hacia la intersección a 40 mph. En un momento, el coche con rumbo al norte es 3.10 millas al norte de la intersección, y el coche con rumbo al oeste es 4/10 millas al este de la intersección. En este punto, la rapidez es la distancia entre los coches cambiantes?
Dibuje un diagrama.
Etiquetar el diagrama con cualquier inmutable números y variables asignar a cualquier cambiar cosas. (Tenga en cuenta que los números 0,3 y 0,4 están en paréntesis para indicar que son no valores que no cambian.)
Lista de todos los tipos dados y la tasa desconocida.
Escriba la fórmula que relaciona las variables en el problema: x, y, y s.
Hay un triángulo rectángulo en el diagrama, para que utilice el teorema de Pitágoras:
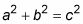
Para este problema, X y y son las patas del triángulo rectángulo, y s es la hipotenusa, por lo
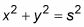
Diferenciar con respecto a t.
Use el teorema de Pitágoras de nuevo para despejar s.
X = 0,4
y = 0,3
Usted puede rechazar la respuesta negativa porque s obviamente, tiene una longitud positiva. Así s = 0,5.
Ahora que tienes todo lo necesario para sustituir en el resultado la diferenciación y resuelve para ds / dt.
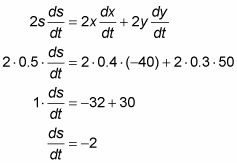
Esta respuesta negativa significa que la distancia, s, es decreciente. Por lo tanto, cuando el coche A es 3 cuadras al norte de la intersección y el coche B está a 4 cuadras al este de la intersección, la distancia entre ellos está disminuyendo a un ritmo de 2 mph.
-
¿Cómo medir los triángulos -
Cálculo: cómo resolver los problemas de diferenciación -
Cómo hacer un problema relacionado tasa implica una pelota de béisbol en movimiento -
¿Cómo encontrar el cambio de distancia entre dos objetos móviles -
Tasas relacionadas: el canal de problema de comida para cerdos -
Tasas relacionadas: el problema del globo en expansión
Aplicando el teorema de Pitágoras El teorema de Pitágoras se ha conocido durante al menos 2.500 años. Se utiliza el teorema de Pitágoras cuando se sabe las longitudes de dos lados de un triángulo rectángulo y quiere averiguar la longitud del tercer lado.El teorema de…
Descubriendo ternas pitagóricas El teorema de Pitágoras es sin duda uno de los teoremas más famosos de toda la matemática. Matemáticos y laicos por igual han estudiado durante siglos, y la gente ha demostrado de muchas maneras diferentes. (Incluso el presidente James Garfield…
¿Cómo encontrar el área de la intersección de dos polígonos GeoMaster en la calculadora gráfica TI-84 no puede encontrar el área de un polígono formado por la intersección de otros dos polígonos porque GeoMaster no sabe que está ahí. Para obtener GeoMaster para encontrar el área de la intersección,…
¿Cómo resolver un problema-tangente común los problema-tangente común se nombra para el segmento única tangente que es tangente a dos círculos. Su objetivo es encontrar la longitud de la tangente. Estos problemas son un poco complicado, pero deben hacer que poca dificultad si se utiliza…
¿Cómo resolver problemas con el teorema de altitud-0n-hipotenusa En un triángulo rectángulo, la altitud que es perpendicular a la hipotenusa tiene una propiedad especial: crea dos triángulos más pequeños de derecha que son a la vez similar al triángulo original derecha.Altitud-on-Hipotenusa Teorema: Si una…
¿Cómo encontrar la distancia a través de un estanque La trigonometría es muy útil para encontrar las distancias que no se puede llegar a medir. Imagina que quieres cadena un cable diagonal a través de un estanque (para que pueda adjuntar un montón de línea de pesca y anzuelos). La distancia…
¿Cómo se mide la velocidad de un coche alrededor de una pista de carreras Un coche de carreras va alrededor de una pista circular. Un fotógrafo de pie en el centro de la pista toma una foto, se convierte de 80 grados, y luego toma otra foto 10 segundos después. Si la pista tiene un diámetro de 1.2 millas, lo rápido…
Definir el movimiento tanto en distancia y dirección En física, el movimiento que se produce en el mundo real es a menudo en dos dimensiones. Como resultado de ello, es necesario encontrar tanto la distancia y dirección viajaron a contar toda la historia.Si desea examinar el movimiento en dos…
¿Cómo encontrar el ángulo y la magnitud de un vector En la física, a veces tienes que encontrar el ángulo y la magnitud de un vector en lugar de los componentes. Para conocer la magnitud, se utiliza el teorema de Pitágoras. Y para encontrarse utiliza la función tangente inversa (o seno inverso o…
Física - desplazamiento y velocidad Imagine que un coche comienza viajando por una carretera después de comenzar a partir de una señal específica. Para conocer la posición exacta del coche después de haber recorrido una distancia determinada, lo que necesita saber no sólo las…
¿Cómo resolver problemas de viaje en el ASVAB Verá problemas de viaje en el ASVAB. Problemas viajes involucran el uso de la fórmula de la distancia, d = rt, dónde d es la distancia, r es la tasa, y t es el momento. En general, los problemas vienen en tres sabores básicos: viaja lejos el uno…
Emt examen: consejos para llevar a cabo el rescate de luz Dependiendo de donde usted trabaja (y para definitivamente para el examen EMT), es posible que tenga que saber cómo llevar a cabo las operaciones de rescate sencillos. Estos pueden incluir romper una ventana de coche de forma segura con un punzón…