¿Cómo resolver problemas de viaje en el ASVAB

Verá problemas de viaje en el ASVAB. Problemas viajes involucran el uso de la fórmula de la distancia, d

= rt, dónde d es la distancia, r es la tasa, y t es el momento. En general, los problemas vienen en tres sabores básicos: viaja lejos el uno del otro, viajando en la misma dirección, y viajando en ángulos de 90 grados.

Viajando de distancia el uno del otro

Cuando dos planos (o trenes, coches, personas, o incluso errores) viajan en direcciones opuestas, aumentan la distancia entre ellos en proporción directa. Para resolver este tipo de problemas, a calcular la distancia recorrida desde el punto de partida para cada plano (o en tren, coche, persona o error).

Un tren viaja hacia el norte a 60 mph. Tren B viaja al sur a 70 mph. Si ambos trenes salen de la estación, al mismo tiempo, a qué distancia van a estar al final de dos horas?

Para resolver este problema, a calcular la distancia recorrida por el tren A y luego la distancia recorrida por el tren B y agregar los resultados juntos.

La fórmula de la distancia es d = rt. La velocidad de desplazamiento para el tren A es de 60 kilómetros por hora, y se desplaza por dos horas:

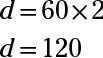
Un tren viaja 120 millas durante el período de dos horas.

Cuando se utiliza la fórmula de la distancia, hay que prestar atención a las unidades de medida. Recuerde la regla de manzanas-y-naranjas. Si la tasa (r) Se expresa en kilómetros por hora, su resultado (d) Será kilómetros. Si la tasa (r) Se expresa como millas por segundo, debe convertirlo a mph o convertir el tiempo (t) A segundos.

La velocidad de desplazamiento para el tren B es de 70 kilómetros por hora, y también viaja durante dos horas:

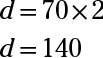
Tren B viaja 140 millas durante el período de dos horas.

Tren A es de 120 millas de la estación de tren y B es de 140 millas de la estación, en la dirección opuesta. Los dos trenes son 120 + 140 = 260 millas de distancia.

Viajando en la misma dirección

Si dos trenes viajan en la misma dirección como los demás pero a diferentes velocidades, un tren viaja más lejos en el mismo tiempo que los otros viajes. La distancia entre los dos trenes es la diferencia entre la distancia recorrida por el tren A y la distancia recorrida por el tren B.

Un tren viaja hacia el norte a 60 mph. Tren B también viaja hacia el norte, en una pista paralela, a 70 mph. Si ambos trenes salen de la estación, al mismo tiempo, a qué distancia van a estar al final de dos horas?

Un tren viajó 120 millas, y el tren B viajó 140 millas. Debido a que están viajando en la misma dirección, se resta para encontrar la distancia que los separaba: 140 - 120 = 20. Los dos trenes están a 20 millas de distancia.

Viajando en ángulos de 90 grados

Algunos problemas de viaje implican dos personas o cosas que se mueven en ángulo de 90 grados y luego stopping- el problema entonces le pregunta qué es la distancia (en línea recta) entre las dos personas o cosas, lo que significa que necesita utilizar la fórmula de distancia y un poco de geometría básica.

Un tren viaja hacia el norte a 60 mph. Tren B viaja de este a 70 mph. Ambos trenes viajan durante dos horas. Entonces una abeja vuela de tren A y aterriza en tren B. Suponiendo que la abeja volando en línea recta, lo hizo con mucho, el viaje de tránsito entre los dos trenes?

Un tren viaja 120 millas, y el tren B recorre una distancia de 140 millas.

Debido a que los trenes están viajando en ángulos de 90 grados (uno al norte y otro al este), las líneas de la forma de viaje de dos lados de un triángulo rectángulo.

El teorema de Pitágoras dice que si usted sabe la longitud de dos lados de un triángulo rectángulo, se puede encontrar la longitud del tercer lado mediante el uso de la fórmula la² + b² = c²:

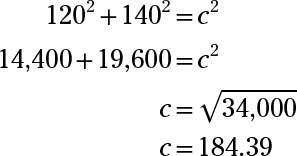
La abeja vuela 184.39 millas.

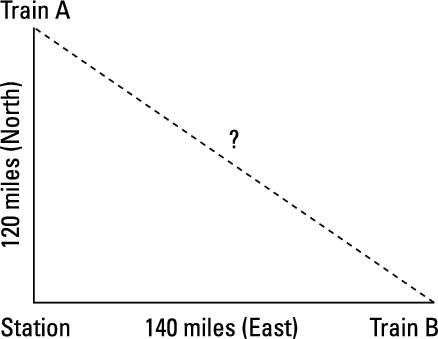
Encontrar la raíz cuadrada de un número muy grande puede ser una tarea desalentadora, especialmente porque usted no tiene una calculadora disponible durante el ASVAB. Al llegar a este punto de la ecuación, simplemente cuadrar las posibles respuestas para ver cuál funciona a menudo es más fácil.