Razonamiento aritmético ejemplos de preguntas subprueba ASVAB

Use estas preguntas ASVAB para acostumbrarse a la estructura de la prueba general y para la práctica algunos de los conceptos que usted necesita saber para esta prueba. Cuando esté listo, tomar un examen completo de la práctica soplado.

Ejemplos de preguntas

1. Si las manzanas están en venta a 15 por $ 3, ¿cuál es el costo de cada manzana?

2. (A) 50 # 162;

3. (B) 25 # 162;

4. (C) 20 # 162;

5. (D) 30 # 162;

6. Un suboficial desafió a su pelotón de 11 mujeres alistados a batir su récord de realizar un entrenamiento de 26 millas en cuatro horas. Si todas las mujeres alistados coinciden con su expediente, la cantidad de millas Tendrán correr?

7. (A) 71,5 millas

8. (B) 6.5 millas

9. (C) 286 millas

10. (D) 312 millas

11. Margaret obtiene su corte de pelo y de color en un salón caro de la ciudad. Se espera que dejar una propina del 15 por ciento para los servicios. Si un corte de pelo es de $ 45 y un tratamiento del color es de $ 150, la cantidad de una punta debe dejar Margaret?

12. (A) $ 22.50

13. (B) $ 29.25

14. (C) $ 20.00

15. (D) $ 195.00

16. Una bolsa de arena tiene 1 pie cúbico de arena. ¿Cuántas bolsas de arena se necesitan para llenar una caja de arena cuadrado que mide 5 pies de largo y 1 pie de altura?

17. (A) 5 bolsas

18. (B) 10 bolsas

19. (C) 15 bolsas

20. (D) 25 bolsas

21. El día Samantha llegó al campo de entrenamiento, la temperatura alcanzó una máxima de 90 grados a la sombra y una mínima de -20 grados por la noche en el cuartel. ¿Cuál es el promedio entre las altas y bajas temperaturas para el día?

22. (A) 35 grados

23. (B) 45 grados

24. (C) de 70 grados

25. (D) 62 grados

26. Farmer Bet ha recibido una oferta para vender su granja de 320 acres por $ 3,000 por acre. Ella está de acuerdo en dar al comprador $ 96.000 el valor de la tierra. ¿Qué fracción de terreno del granjero Bet es conseguir que el comprador?

27. (A) cuarta

28. (B) 01/10

29. (C) 1/5

30. (D) 2/3

31. Un mapa se dibuja de manera que 1 pulgada equivale a 3 millas. En el mapa, la distancia de Kansas City a Denver es 192.5 pulgadas. ¿Hasta qué punto es el de ida y vuelta de Kansas City a Denver en millas?

32. (A) 192,5 millas

33. (B) 577,5 millas

34. (C) 385 millas

35. (D) 1.155 millas

36. Margaret y Julie pueden vender su tienda por $ 150.000. Planean dividir las ganancias de acuerdo a la relación entre el dinero que cada uno invertido en el negocio. Margaret poner en la mayor cantidad de dinero, en una proporción de 3: 2 a Julie. ¿Cuánto dinero debe Julie obtener de la venta?

37. (A) $ 50.000

38. (B) $ 30.000

39. (C) $ 60.000

40. (D) $ 90.000

41. En el ejército, 1.4 del tiempo de una persona alistado se gasta dormir y comer, 1/12 se gasta en posición de firmes, 16 se gasta mantenerse en forma, y 2.5 está dedicado a trabajar. El resto del tiempo se dedica a discreción de la persona alistado. ¿Cuántas horas por día tiene esta cantidad de tiempo discrecional para?

42. (A) 6 horas

43. (B) 1.6 hora

44. (C) 2.4 hora

45. (D) 3,2 horas

46. Tren A se dirigió hacia el este a 55 mph. Tren B también se dirige hacia el este en una pista adyacente a 70 mph. Al final de cuatro horas, ¿cuánto más entrenará B han viajado de tren de A?

47. (A) 40 millas

48. (B) 50 millas

49. (C) 60 millas

50. (D) 70 millas

Respuestas y explicaciones

Utilice esta clave de respuestas para anotar las preguntas de práctica razonamiento aritmético.

1. C. Divida $ 3 por 15.

2. C. Multiplique 26 x 11. La otra información en la pregunta se irrelevant- que está ahí para hacerle perder.

3. B. Agregar $ 45 y $ 150 y multiplicar el resultado por 15 por ciento, o 0,15.

4. D. La fórmula del volumen de una caja cuadrada o rectangular es v = lwh, así v = 5 x 5 x 1 = 25 pies cúbicos. Cada bolsa tiene 1 pie cúbico de arena.

5. A. Añadir las dos temperaturas dadas y se divide por el número de términos, 2: (90 + -20) 247- # 2 = 70 247- # 2 = 35.

6. B. $ 96.000 dividido por $ 3,000 (el precio por acre) es igual a 32 acres y 32 acres, dividido por 320 acres (el tamaño total de la finca) es igual a 10 por ciento, o un décimo de la tierra.

7. D. Multiplicar 192,5 x 3 para obtener la distancia en millas y luego duplicar la respuesta a la cuenta de ambas piernas del viaje.

8. C. Margaret debe recibir 3/5 del dinero y Julie debe recibir 2/5 del dinero. Las fracciones se calculan mediante la adición de ambos lados de la relación de juntas (3 + 2 = 5) para determinar el denominador. Cada lado de la relación se convierte en un numerador, por lo que la inversión de Margaret puede demostrarse que es 3/5 de la inversión total, y Julie es 2/5 de la inversión total.

   Puede comprobar estas fracciones mediante la adición de 3.5 y 2.5 para obtener 5.5 o 1, que es todo el dinero.) Divida $ 150.000 en 5, y luego multiplicar el resultado por 2 para determinar parte del dinero de Julie.

9. C. Calcular esta respuesta asignando primero un denominador común de 60 a todas las fracciones y el ajuste de los numeradores en consecuencia:

   

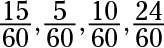
   Añadir las fracciones para averiguar cuánto tiempo se asigna a todas estas tareas. El total es de 54/60, lo que deja 6/60 o 1/10 del día a la discreción de la persona alistado. 1 / 10of 24 horas es de 2,4 horas.

10. C. La fórmula de la distancia es d = rt. Conecte los valores conocidos:

11. Entrene A: d = 55 x 4 = 220 millas

12. Tren B: d = 70 x 4 = 280 millas

    Tren B viajó 280 - 220 = 60 millas más que el tren A.