Anote, tiempo y distancia problemas en el PSAT / NMSQT
Es probable que obtener algunos problemas ritmo, tiempo y distancia en el PSAT / NMSQT. ¿No odias preguntas en el que un chico está impulsando este a 40 millas por hora y un amigo se está moviendo al oeste haciendo 65? Se supone que tienes que averiguar dónde se encuentran y pasan por alto el hecho de que en la vida real que sólo puede llamar a los demás y explicar dónde están.
Pero si usted consigue uno de estos problemas en el PSAT / NMSQT, por lo menos se puede resolver con bastante facilidad. Sólo recuerda esta fórmula: Rcomió x Time = DIstance (IDT).
Un pequeño boceto o un gráfico a menudo le ayuda con preguntas tasa / tiempo / distancia.
He aquí un ejemplo. Su robot toddles a lo largo a una velocidad de 3 pies por minuto durante 30 minutos. Robot de MEGABRAIN zoom a 30 pies por segundo durante 10 minutos. ¿Cuánto más lejos va robot de viajes de MEGABRAIN de su robot?
Para resolver éste, pruebe con un gráfico. Los títulos coinciden con los términos de la fórmula, Tasa x Tiempo = Distancia. Antes de llenar las cajas, sin embargo, estar seguro de que todo coincide. Robot de MEGABRAIN viaja 30 pies por segundo. (Cuidado con estos cambios difíciles en unidades!) Debido a que un minuto tiene 60 segundos, la velocidad de MEGABRAIN es de 1800 pies por minuto.
Ahora usted puede llenar en la tabla. Comience con lo que sabe:
| Tasa | Hora | Distancia | |
|---|---|---|---|
| Su robot | 3 pies por minuto | 30 minutos | |
| Robot de MEGABRAIN | 1800 pies por minuto | 10 minutos |
Ahora rellenar los cuadrados vacíos. El robot va 3 x 30 o 90 pies. Robot de MEGABRAIN viaja 1800 x 10 o 18.000 pies.
| Tasa | Hora | Distancia | |
|---|---|---|---|
| Su robot | 3 pies por minuto | 30 minutos | 90 |
| Robot de MEGABRAIN | 1800 pies por minuto | 10 minutos | 18000 |
Robot de MEGABRAIN viaja 18.000 - 90 pies, o 17.910 pies más lejos que la tuya.
Se le puede pedir lo lejos que están. Si es así, observar si están viajando en la misma dirección o en la dirección opuesta. En la misma dirección, se resta. En la dirección opuesta, se agrega. (Dibuje un vistazo y verás.)
Golpee el camino y tratar estos problemas:
James y Kat están de pie en los extremos opuestos de un campo de fútbol, de 300 pies de distancia el uno del otro. Si Kat camina a una velocidad de 12 pies por segundo, James camina a un ritmo de 8 pies por segundo, y caminan hacia la otra, cuánto tiempo tomará para que ellos se reúnen?
(A) 15 segundo(B) 75 segundo(C) 2 minutos(D) 3 minutos(E) 15 minutos
Dos barcos se reúnen en un lago, y después de los capitanes comparten bocadillos, la cabeza en diferentes direcciones. Las cabezas lancha directamente al este a una velocidad de 36 millas por hora, y el velero va al norte a una velocidad de 15 millas por hora. Si ambos barcos continúan viajando en línea recta, a qué distancia estarán en 2 horas?
(A) 21 millas(B) 39 millas(C) 51 millas(D) 78 millas(E) 100 millas
Alexis se acercó a una velocidad de 3 millas por hora durante 20 minutos y luego se detuvo para hablar por teléfono durante 16 minutos. Después de su conversación telefónica, Alexis se acercó a una velocidad de 5 millas por hora durante el resto de la hora. ¿Cuál fue la velocidad promedio de Alexis sobre la hora?
(A) 2 mph(B) 2,5 mph(C) 3 mph(D) 3,5 mph(E) 4 mph
Ahora compruebe sus respuestas:
A. 15 segundos
Usted sabe que tanto James y Kat están caminando por el mismo período de tiempo, y usted quiere saber lo que el tiempo es, por lo que por el momento, simplemente llamarlo t. James caminará (8 pies / segundo) x t pies (velocidad x tiempo), y Kat caminará (12 pies / segundo) x t los pies. Juntos, caminan 300 pies, por lo que saben que 8t + 12t = 300.
Sume los términos semejantes y se obtiene 20t = 300, y cuando se divide ves que t = 15. Puede pensar unidades recordando que está dividiendo a 300 pies por 20 pies / segundo, lo que equivale a 15 segundos. La opción (A) es su respuesta.
D. 78 millas
IDT y triángulos rectángulos? ¡Puedes hacerlo! Dibuje a ti mismo una imagen primera.
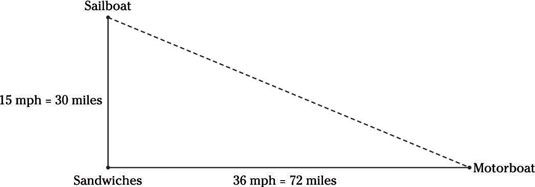
Usted sabe que cada embarcación se desplace durante 2 horas, para que pueda utilizar la IDT para determinar qué tan lejos ha viajado cada uno: 30 millas para el velero y 72 millas de la lancha. Ahora todo lo que tiene que hacer es aplicar el teorema de Pitágoras para averiguar a qué distancia los barcos son: 302 + 722 = d2- 900 + 5184 = d2- d = 78 millas de distancia, opción (D).
C. 3 mph
Para encontrar la velocidad media de Alexis, primero tiene que encontrar la distancia total viajó y el tiempo total que viajaba (estos dos incluye el tiempo que ella se detuvo!). Para la primera parte de su viaje, Alexis viajó durante 20 minutos, o 1/3 de una hora, a una velocidad de 3 millas por hora.
El uso de IDT, se puede ver que ella viajó 1 milla durante esos primeros 20 minutos. Alexis No logró el progreso hacia adelante durante su conversación telefónica, por lo que sabe que ella pasó los primeros 36 minutos ir de 1 milla. En los 24 minutos para el final (60 - 36 = 24 minutos) de la hora, Alexis se acercó a una velocidad de 5 millas por hora.
24 minutos fuera de 60 es el mismo que 2/5 del de una hora. El uso de IDT, (2/5) x 5 = 2 millas de recorrido en los últimos 24 minutos, para un total de 3 millas en 60 minutos. Esto hace que la velocidad promedio de Alexis 3 millas por hora, opción (C).






