¿Cómo encontrar el ángulo y la magnitud de un vector

En la física, a veces tienes que encontrar el ángulo y la magnitud de un vector en lugar de los componentes. Para conocer la magnitud, se utiliza el teorema de Pitágoras. Y para encontrar

se utiliza la función tangente inversa (o seno inverso o coseno).

Por ejemplo, supongamos que usted está buscando un hotel que está a 20 millas al este y luego 20 millas al norte. Desde su ubicación actual, ¿cuál es el ángulo (medido desde el este) de la dirección del hotel, y hasta qué punto se encuentra el hotel? Usted puede escribir este problema en notación vectorial, así:

Paso 1: (20, 0)

Paso 2: (0, 20)

Cuando la adición de estos vectores en conjunto, se obtiene este resultado:

(20, 0) + (0, 20) = (20, 20)

El vector resultante es (20, 20). Esa es una manera de especificar un vector - utilizar sus componentes. Pero este problema no está pidiendo los resultados en términos de componentes. La pregunta quiere saber el ángulo y la distancia hasta el hotel.

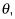
En otras palabras, mirando a la figura anterior, el problema se pregunta,

Si conoces componentes verticales y horizontales de un vector, la búsqueda de la magnitud del vector no es tan difícil porque usted sólo tiene que encontrar la hipotenusa de un triángulo rectángulo. Puedes usar el teorema de Pitágoras (X² + y² = h²), Resuelto por h:

La conexión de los números que da

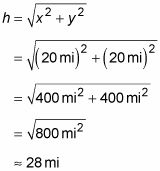
Tenga en cuenta que cuando se conocen los componentes horizontal y vertical de un vector, puede utilizar la tangente para encontrar el ángulo debido

Todo lo que tienes que hacer es tomar la tangente inversa de y/X:

Supongamos que usted conduce 20 millas al este y 20 millas al norte. He aquí cómo usted encuentra

el ángulo entre la posición original y el final de una:

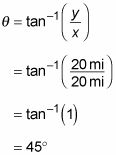
Así que el hotel está situado a 28 millas de distancia en un ángulo de 45 grados.

Tenga cuidado al hacer los cálculos con tangentes inversas, porque los ángulos que difieren en 180 grados tienen la misma tangente. Cuando usted toma la tangente inversa, puede que tenga que añadir o restar 180 grados para conseguir el ángulo real que desea. El botón tangente inversa en su calculadora siempre le dará un ángulo entre 90 grados y 90 grados. Si el ángulo no es en este rango, entonces usted tiene que añadir o restar 180 grados.

Para este ejemplo, la respuesta de 45 grados debe ser correcta. Pero considere una situación en la que se necesitaría para sumar o restar 180 grados: Suponga que usted camina por completo la dirección opuesta al hotel. Se puede caminar 20 millas al oeste y 20 millas al sur (X = -20 Millas, y = -20 Millas), por lo que si se utiliza el mismo método para calcular el ángulo, se obtiene lo siguiente:

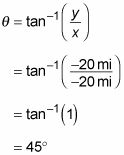
Usted recibe la misma respuesta para el ángulo a pesar de que usted está caminando en la dirección opuesta por completo como antes! Eso es porque las tangentes de los ángulos que difieren en 180 grados son iguales. Pero si nos fijamos en los componentes del vector (X = -20 Millas, y = -20 Millas), ambos son negativos, por lo que el ángulo debe estar entre -90 grados y -180 grados. Si se resta 180 grados de su respuesta de 45 grados, se obtiene -135 grados, que es el ángulo real medido desde el eje x positivo en la dirección hacia la derecha.

Alternativamente, usted podría pensar que ya que los componentes del vector son negativos, debe ser entre 180 grados y 270 grados. A continuación, añadir 180 grados a su resultado y obtener 225 grados, que se mide desde el eje x positivo en la dirección hacia la izquierda.

Así pues, que el ángulo es correcto, 225 grados o -135 grados? ¡Ambas cosas! Ya sea que usted se mueve en sentido antihorario 225 grados o 135 grados en sentido horario desde el eje x positivo, se termina la partida en la misma dirección.