Cómo agregar vectores juntos
Se le pide con frecuencia para añadir vectores en la resolución de problemas de física. Para sumar dos vectores, se colocan la cabeza a la cola y luego encontrar la duración y magnitud del resultado. El orden en que se agregan los dos vectores no importa.
Por ejemplo, supongamos que te diriges a la gran convención de la física y se les ha dicho que vaya a 20 millas al norte y luego 20 millas hacia el este hasta llegar allí. ¿A qué ángulo es el centro de convenciones de su ubicación actual, y qué tan lejos está?
Usted puede escribir estos dos vectores como este (donde este se encuentra a lo largo del positivo X eje):
(0, 20)(20, 0)
En este caso, es necesario agregar estos dos vectores, y usted puede hacer eso simplemente añadiendo su X y y componentes por separado:
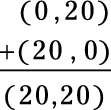
Haga sus cálculos, y el vector resultante es (20, 20). Usted acaba de completar una suma de vectores. Pero la pregunta es para el vector en términos de magnitud / ángulo, no coordinar términos. Entonces, ¿cuál es la magnitud del vector de usted a la convención de la física? Usted puede ver la situación en la siguiente figura, donde tienes X y y y desee encontrar v.
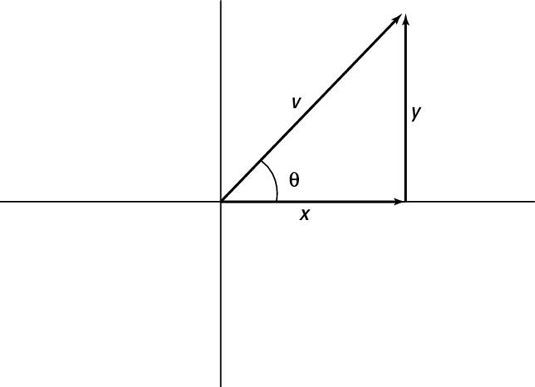
descubrimiento v no es tan difícil porque se puede utilizar el teorema de Pitágoras:
Conecte los números para obtener
Así que la convención es de 28,3 millas de distancia. ¿Qué pasa con el ángulo theta? Sabes
theta = tan-1(y/X) = Tan-1(20/20) = 45 grados
Y eso es todo - que ahora sabemos que la convención es de 28,3 millas de distancia en un ángulo de 45 grados.
Ejemplo de pregunta
Añadir los dos vectores en la siguiente figura. Uno tiene una magnitud 5.0 y ángulo de 45 grados, y el otro tiene una magnitud 7,0 y el ángulo de 35 grados.
La respuesta correcta es la magnitud 12,0, ángulo de 39 grados.
Resolver los dos vectores en sus componentes. Para la primera vector, aplicar la ecuación vX = v cos theta para encontrar el X de coordenadas. Eso es 5.0 cos 45 grados = 3.5.
Aplicar la ecuación vy = v theta pecado para encontrar el y de coordenadas de la primera vector. Eso es 5.0 pecado 45 grados, o 3.5. Así que el primer vector es (3.5, 3.5) en forma de coordenadas.
Para el segundo vector, aplicar la ecuación vX = v cos theta para encontrar el X de coordenadas. Eso es 7,0 cos 35 grados = 5,7.
Aplicar la ecuación vy = v theta pecado para encontrar el y de coordenadas del segundo vector. Eso es 7.0 pecado 35 grados = 4.0. Así que el segundo vector es (5.7, 4.0) en forma de coordenadas.
Para añadir los dos vectores, añadirlos en coordinar formulario: (3.5, 3.5) + (5,7, 4,0) = (9.2, 7.5).
Convertir (9.2, 7.5) en forma de magnitud / ángulo. Aplicar la ecuación de theta = tan-1(y/X) Para encontrar el ángulo, que es tan-1(7,5 / 9,2) = tan-1(0,82) = 39 grados.
Aplicar la ecuación
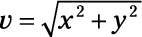
para encontrar la magnitud, que es
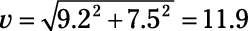
Conversión a dos dígitos significativos le da 12.
Preguntas de práctica
Añadir un vector cuya magnitud es 13.0 y el ángulo es de 27 grados con respecto a aquel cuya magnitud es 11.0 y el ángulo es de 45 grados.
Añadir un vector cuya magnitud es 16.0 y el ángulo es de 56 grados con respecto a aquel cuya magnitud es 10.0 y el ángulo es de 25 grados.
Añadir dos vectores: Vector uno tiene una magnitud 22,0 y el ángulo de 19 grados, y el vector de dos tiene una magnitud 19,0 y un ángulo de 48 grados.
Añadir un vector cuya magnitud es 10.0 y el ángulo es de 257 grados a aquel cuya magnitud es 11.0 y el ángulo es de 105 grados.
A continuación se presentan las respuestas a las preguntas de la práctica:
Magnitud 23.7, ángulo de 35 grados
Para el primer vector, utilice la ecuación vX = v cos theta para encontrar la X coordinar: 13.0 x cos 27 grados = 11,6.
Utilice la ecuación vy = v theta pecado para encontrar la y coordenadas del primer vector: 13,0 x sen 27 grados, o 5,90. Así que el primer vector es (11.6, 5.90) en forma de coordenadas.
Para el segundo vector, utilice la ecuación vX = v cos theta para encontrar la X coordinar: 11.0 x cos 45º = 7.78.
Utilice la ecuación vy = v theta pecado para encontrar la y coordenadas del segundo vector: 11,0 x sen 45 ° = 7,78. Así que el segundo vector es (7,78, 7,78) en forma de coordenadas.
Añadir los dos vectores en coordenadas forma: (11.6, 5.90) + (7.78, 7.78) = (19.4, 13.7).
Convertir (19.4, 13.7) en forma de magnitud / ángulo. Utilice la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(13,7 / 19,4) = tan-1(0,71) = 35 grados.
Aplicar la ecuación
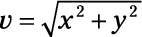
para encontrar la magnitud, que es
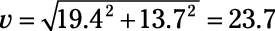
Magnitud 25.1, ángulo de 44 grados
Para el primer vector, utilice la ecuación vX = v cos theta para encontrar la X coordinar: 16.0 x cos 56 grados = 8,95.
Utilice la ecuación vy = v theta pecado para encontrar la y coordenadas del primer vector: 16,0 x sen 56 grados, o 13.3. Así que el primer vector es (8.95, 13.3) en forma de coordenadas.
Para el segundo vector, utilice la ecuación vX = v cos theta para encontrar la X coordinar: 10,0 x cos 25 grados = 9.06.
Utilice la ecuación vy = v theta pecado para encontrar la y coordenadas del segundo vector: 10,0 x sen 25 grados = 4.23. Así que el segundo vector es (9.06, 4.23) en forma de coordenadas.
Añadir los dos vectores en coordenadas forma: (8.95, 13.3) + (9.06, 4.23) = (18.0, 17.5).
Convertir el vector (18.0, 17.5) en forma de magnitud / ángulo. Utilice la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(17,5 / 18,0) = tan-1(0,97) = 44 grados.
Aplicar la ecuación
para encontrar la magnitud, que es
Magnitud 39.7, ángulo de 32 grados
Para el primer vector, utilice la ecuación vX = v cos theta para encontrar la X coordinar: 22.0 x cos 19 grados = 20,8.
Utilice la ecuación vy = v theta pecado para encontrar la y coordenadas del primer vector: 22,0 x sen 19 grados, o 7,16. Así que el primer vector es (20.8, 7.16) en forma de coordenadas.
Para el segundo vector, utilice la ecuación vX = v cos theta para encontrar la X coordinar: 19.0 x cos 48 grados = 12,7.
Utilice la ecuación vy = v theta pecado para encontrar la y coordenadas del segundo vector: 19,0 x sen 48 grados = 14,1. Así que el segundo vector es (12.7, 14.1) en forma de coordenadas.
Añadir los dos vectores en coordenadas forma: (20.8, 7.16) + (12.7, 14.1) = (33.5, 21.3).
Convertir el vector (33.5, 21.3) en forma de magnitud / ángulo. Utilice la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(21,3 / 33,5) = tan-1(0,64) = 32 grados.
Aplicar la ecuación
para encontrar la magnitud, que es
Magnitud 5.2, ángulo de 170 grados
1.Para el primer vector, utilice la ecuación vX = v cos theta para encontrar la X coordinar: 10,0 x cos 257 grados = -2.25.
Utilice la ecuación vy = v theta pecado para encontrar la y coordenadas del primer vector: 10,0 x sen 257 grados, o -9.74. Así que el primer vector es (-2,25, -9,74) Forma de coordenadas.
Para el segundo vector, utilice la ecuación vX = v cos theta para encontrar la X coordinar: 11.0 x cos 105 grados = -2.85.
Utilice la ecuación vy = v theta pecado para encontrar la y coordenadas del segundo vector: 11,0 x sen 105 grados = 10,6. Así que el segundo vector es (-2,85, 10.6) en forma de coordenadas.
Añadir los dos vectores en coordenadas formulario: (-2.25, -9.74) + (-2,85, 10,6) = (-5.10, 0.86).
Convertir el vector (-5.10, 0.86) en forma de magnitud / ángulo. Utilice la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(0,86 / -5,10) = tan-1(-0,17) = 170 grados. Porque X es negativo y y es positivo, este vector debe estar en el segundo cuadrante.
Aplicar la ecuación
para encontrar la magnitud, que es
Cálculo de la fuerza neta y aceleración Newton dice sigmaF = mla, lo que significa que agrega todos los vectores de fuerza en conjunto para obtener la fuerza neta. Eso es lo que por lo general funciona cuando se tiene que averiguar F = mamá problemas de la física. A menudo, una serie de…
Cálculo del vector resultante de dos vectores de desplazamiento En la física, al igual que usted puede agregar dos números para obtener un tercer número, puede añadir dos vectores de obtener un resultante vector. Para demostrar que va a añadir dos vectores, puso las flechas juntos para que se parte de…
La fuerza es un vector Fuerza, como el desplazamiento, velocidad y aceleración, es una cantidad vectorial, que es la razón por la segunda ley de Newton se escribe como sigmaF = ma. Poner en palabras, se dice que la suma vectorial de las fuerzas que actúan sobre un…
Cómo calcular la velocidad de un objeto en función de su desplazamiento En la física, la velocidad, que es la tasa de cambio de posición (o la velocidad en una dirección particular), es un vector. Imagine que usted acaba de golpear una bola de tierra en el diamante de béisbol y se está ejecutando a lo largo de la…
Cómo calcular el desplazamiento de un objeto en movimiento en dos dimensiones En la física, el desplazamiento, que es un cambio de posición, tiene una magnitud y una dirección asociada con él. Cuando usted tiene un cambio de posición en una dirección particular y de una distancia determinada, éstos se dan por la…
Cómo crear un vector Un vector es una combinación de exactamente dos valores: una magnitud (como la velocidad de un objeto en movimiento) y una dirección (tal como la dirección de un objeto en movimiento). Todo tipo de cosas se pueden describir con vectores,…
¿Cómo encontrar componentes de un vector Puede convertir de la manera magnitud / ángulo de la especificación de un vector para la forma de coordenadas de expresión. Si lo hace, es esencial para los tipos de operaciones que puede esperar para ejecutar en vectores, tales como cuando se…
¿Cómo encontrar magnitud y dirección de un vector Si te dan las componentes de un vector, como (3, 4), se puede convertir fácilmente a la forma en magnitud / ángulo de expresar los vectores usando la trigonometría.Por ejemplo, echar un vistazo a el vector en la imagen.Supongamos que te dan las…
¿Cómo encontrar el ángulo y la magnitud de un vector En la física, a veces tienes que encontrar el ángulo y la magnitud de un vector en lugar de los componentes. Para conocer la magnitud, se utiliza el teorema de Pitágoras. Y para encontrarse utiliza la función tangente inversa (o seno inverso o…
¿Cómo encontrar componentes del vector En la física, cuando se rompe un vector en sus partes, las partes se llaman su componentes. Por ejemplo, en el vector (4, 1), el X-eje (horizontal) componente es 4, y el y-(vertical) componente es 1. Por lo general, un problema de física le da un…
Cómo manejar la velocidad como un vector La velocidad es un vector, y como tal, tiene una magnitud y una dirección asociada con él. Supongamos que estás en un automóvil que viaja hacia el este a 88 metros / segundo cuando se empieza a acelerar el norte a 5,0 metros / segundo2 para 10,0…
Como restar vectores Usted no viene a través del vector resta muy a menudo en problemas de física, pero sí aparecerá. Para restar dos vectores, que puso sus pies (o colas, las partes no puntiagudos) juntos- entonces dibujar el vector resultante, que es la diferencia…