Cálculo del vector resultante de dos vectores de desplazamiento
En la física, al igual que usted puede agregar dos números para obtener un tercer número, puede añadir dos vectores de obtener un resultante vector. Para demostrar que va a añadir dos vectores, puso las flechas juntos para que se parte de flechas donde los otros extremos de flecha. La suma es una nueva flecha que comienza en la base de la primera flecha y termina en la cabeza (extremo puntiagudo) de la otra.
Considere un ejemplo usando vectores de desplazamiento. LA vector de desplazamiento da el cambio de posición: la distancia desde el punto inicial hasta el punto final es la magnitud del vector de desplazamiento y la dirección recorrida es la dirección del vector de desplazamiento.
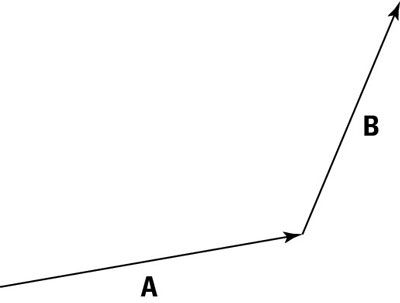
Supongamos, por ejemplo, que un transeúnte le dice que para llegar a su destino, usted primero tiene que seguir vectorial LA y luego vector B. Justo donde es ese destino? Usted trabaja este problema al igual que encuentre el destino en la vida cotidiana. En primer lugar, usted conduce hasta el final del vector LA, y desde ese punto, usted conduce hasta el final del vector B, así como se ve en la figura anterior.
Al llegar al final del vector B, hasta qué punto está usted de su punto de partida? Para averiguarlo, se dibuja un vector, C, desde su punto de partida (pie, o la cola, del primer vector) a su punto (jefe del segundo vector) final, como se ve en la siguiente figura.
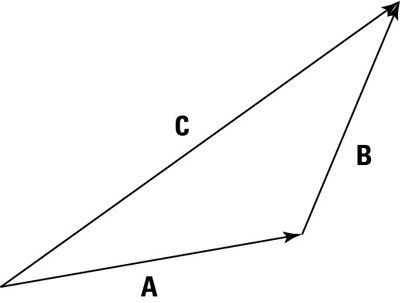
Este nuevo vector representa su viaje completo, de principio a fin. En otras palabras, C = LA + B. El vector C se llama la suma, el resultado, o el vector resultante.
Adición y sustracción de vectores Puede sumar y restar vectores en un gráfico al comenzar un vector en el punto final de otro vector. Sumar y restar vectores de componente a componente, de la siguiente manera:Al agregar o restar dos vectores, el resultado es un…
Cálculo de magnitud con vectores Los vectores se utilizan comúnmente para modelar las fuerzas como el viento, las corrientes marinas, la gravedad y el electromagnetismo. Cálculo de la magnitud de los vectores es esencial para todo tipo de problemas donde las fuerzas…
Encontrar el vector unitario de un vector Cada vector no nulo tiene un correspondiente vector unitario, que tiene la misma dirección que la del vector pero una magnitud de 1. Para encontrar el vector unitario u del vectordivides ese vector por su magnitud como sigue:Tenga en cuenta que…
Encuentra la pendiente y construir un vector con GeoMaster GeoMaster en la calculadora gráfica TI-84 Plus ofrece varias funciones de la MED menú, incluyendo la Cuesta abajo herramienta y la Vector Sum herramienta. los Cuesta abajo herramienta en el MED menú se puede utilizar para encontrar la pendiente…
Cómo construir vectores en r LA vector es el tipo más simple de estructura de datos en el manual de R. El R define un vector como se " una sola entidad que consiste en una colección de cosas ". Una colección de números, por ejemplo, es un vector numérico - los primeros…
Cómo repetir vectores en r En R, puede combinar un vector consigo mismo si quieres repetirlo, pero si quieres repetir los valores de un vector en muchas ocasiones, el uso de la c () la función se convierte en un poco práctico. R hace la vida más fácil al ofrecerle una…
Cómo agregar vectores en una cuadrícula Puede utilizar los componentes de vectores para agregar vectores juntos utilizando una cuadrícula. Si lo hace, reduce el problema de la adición de vectores a una simple combinación de la adición de números juntos, lo cual es muy útil cuando a…
Cómo agregar vectores juntos Se le pide con frecuencia para añadir vectores en la resolución de problemas de física. Para sumar dos vectores, se colocan la cabeza a la cola y luego encontrar la duración y magnitud del resultado. El orden en que se agregan los dos vectores…
Cómo calcular la velocidad de un objeto en función de su desplazamiento En la física, la velocidad, que es la tasa de cambio de posición (o la velocidad en una dirección particular), es un vector. Imagine que usted acaba de golpear una bola de tierra en el diamante de béisbol y se está ejecutando a lo largo de la…
Cómo crear un vector Un vector es una combinación de exactamente dos valores: una magnitud (como la velocidad de un objeto en movimiento) y una dirección (tal como la dirección de un objeto en movimiento). Todo tipo de cosas se pueden describir con vectores,…
¿Cómo encontrar componentes de un vector Puede convertir de la manera magnitud / ángulo de la especificación de un vector para la forma de coordenadas de expresión. Si lo hace, es esencial para los tipos de operaciones que puede esperar para ejecutar en vectores, tales como cuando se…
¿Cómo encontrar magnitud y dirección de un vector Si te dan las componentes de un vector, como (3, 4), se puede convertir fácilmente a la forma en magnitud / ángulo de expresar los vectores usando la trigonometría.Por ejemplo, echar un vistazo a el vector en la imagen.Supongamos que te dan las…