¿Cómo encontrar magnitud y dirección de un vector
Si te dan las componentes de un vector, como (3, 4), se puede convertir fácilmente a la forma en magnitud / ángulo de expresar los vectores usando la trigonometría.
Por ejemplo, echar un vistazo a el vector en la imagen.
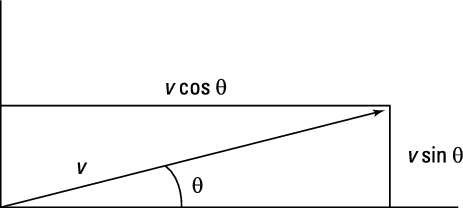
Supongamos que te dan las coordenadas del extremo del vector y quiere encontrar su magnitud, v, y el ángulo, theta. Debido a su conocimiento de la trigonometría, ya sabes
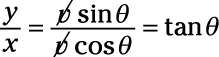
Dónde theta bronceado es la tangente del ángulo. Esto significa eso
theta = tan-1(y/X)
Supongamos que las coordenadas del vector son (3, 4). Usted puede encontrar el ángulo theta como el bronceado-1(4/3) = 53 grados.
Puedes usar el teorema de Pitágoras para encontrar la hipotenusa - la magnitud, v - del triángulo formado por x, y, y v:
Conecte los números para este ejemplo para obtener
Así que si usted tiene un vector dado por las coordenadas (3, 4), su magnitud es 5, y su ángulo es de 53 grados.
Ejemplo de pregunta
Convertir el vector dado por las coordenadas (1,0, 5,0) en formato de magnitud / ángulo.
La respuesta correcta es la magnitud 5,1, ángulo de 79 grados.
Aplicar el teorema de Pitágoras para encontrar la magnitud. Conecte los números para obtener 5.1.
Aplicar la ecuación de theta = tan-1(y/X) Para encontrar el ángulo. Conecte los números para obtener bronceado-1(5,0 / 1,0) = 79 grados.
Preguntas de práctica
Convertir el vector (5.0, 7.0) en forma de magnitud / ángulo.
Convertir el vector (13.0, 13.0) en forma de magnitud / ángulo.
Convertir el vector (-1.0, 1.0) en forma de magnitud / ángulo.
Convertir el vector (-5,0, -7,0) en forma de magnitud / ángulo.
A continuación se presentan las respuestas a las preguntas de la práctica:
Magnitud 8.6, ángulo de 54 grados
Aplicar la ecuación
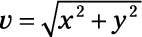
para encontrar la magnitud, que es 8,6.
Aplicar la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(7,0 / 5,0) = 54 grados.
Magnitud 18.4, ángulo de 45 grados
Aplicar la ecuación
para encontrar la magnitud, que es 18,4.
Aplicar la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(13,0 / 13,0) = 45 grados.
Magnitud 1.4, ángulo de 135 grados
Aplicar la ecuación
para encontrar la magnitud, que es 1,4.
Aplicar la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(1,0 / -1,0) = -45 grados.
Sin embargo, tenga en cuenta que el ángulo debe ser realmente entre 90 grados y 180 grados debido a que el primer componente del vector es negativo y el segundo es positivo. Eso significa que usted debe agregar 180 grados a -45 grados, que le da 135 grados (la tangente de 135 grados es también 1.0 / -1.0 = -1,0).
Magnitud 8.6, ángulo de 234 grados
Aplicar la ecuación
para encontrar la magnitud, que es 8,6.
Aplicar la ecuación theta = tan-1 (y / x) para encontrar el ángulo: tan-1 (-7,0 / -5,0) = 54 grados.
Sin embargo, tenga en cuenta que el ángulo debe ser realmente entre 180 grados y 270 grados debido a que ambos componentes del vector son negativos. Eso significa que usted debe agregar 180 grados a 54 grados, que le da 234 grados (la tangente de 234 grados es también -7.0 / -5.0 = 7,0 / 5,0).
Componer un vector de fuerza resultante de múltiples vectores Despejando la fuerza resultante creada cuando varias fuerzas actúan sobre un cuerpo implica varios pasos. Las medidas incluyen el uso de las herramientas de matemáticas y trigonometría para trabajar con vectores de fuerza. El uso de un enfoque…
Cálculo de la fuerza neta y aceleración Newton dice sigmaF = mla, lo que significa que agrega todos los vectores de fuerza en conjunto para obtener la fuerza neta. Eso es lo que por lo general funciona cuando se tiene que averiguar F = mamá problemas de la física. A menudo, una serie de…
Colisiones en dos dimensiones Las colisiones pueden tener lugar en dos dimensiones. Por ejemplo, pelotas de fútbol pueden pasar de cualquier manera en un campo de fútbol, no sólo a lo largo de una sola línea. Balones de fútbol puede llegar a ir al norte o al sur, al…
La conversión entre ángulos Estudio en física por lo general comienza con movimiento lineal, que es el movimiento en línea recta. Gran parte de la física se centra en el movimiento angular, sin embargo, que es el movimiento de los objetos en los alrededores de círculos o…
La fuerza es un vector Fuerza, como el desplazamiento, velocidad y aceleración, es una cantidad vectorial, que es la razón por la segunda ley de Newton se escribe como sigmaF = ma. Poner en palabras, se dice que la suma vectorial de las fuerzas que actúan sobre un…
Cómo agregar vectores juntos Se le pide con frecuencia para añadir vectores en la resolución de problemas de física. Para sumar dos vectores, se colocan la cabeza a la cola y luego encontrar la duración y magnitud del resultado. El orden en que se agregan los dos vectores…
Cómo calcular la velocidad de un objeto en función de su desplazamiento En la física, la velocidad, que es la tasa de cambio de posición (o la velocidad en una dirección particular), es un vector. Imagine que usted acaba de golpear una bola de tierra en el diamante de béisbol y se está ejecutando a lo largo de la…
Cómo crear un vector Un vector es una combinación de exactamente dos valores: una magnitud (como la velocidad de un objeto en movimiento) y una dirección (tal como la dirección de un objeto en movimiento). Todo tipo de cosas se pueden describir con vectores,…
¿Cómo encontrar componentes de un vector Puede convertir de la manera magnitud / ángulo de la especificación de un vector para la forma de coordenadas de expresión. Si lo hace, es esencial para los tipos de operaciones que puede esperar para ejecutar en vectores, tales como cuando se…
¿Cómo encontrar el ángulo y la magnitud de un vector En la física, a veces tienes que encontrar el ángulo y la magnitud de un vector en lugar de los componentes. Para conocer la magnitud, se utiliza el teorema de Pitágoras. Y para encontrarse utiliza la función tangente inversa (o seno inverso o…
¿Cómo encontrar componentes del vector En la física, cuando se rompe un vector en sus partes, las partes se llaman su componentes. Por ejemplo, en el vector (4, 1), el X-eje (horizontal) componente es 4, y el y-(vertical) componente es 1. Por lo general, un problema de física le da un…
Cómo manejar la velocidad como un vector La velocidad es un vector, y como tal, tiene una magnitud y una dirección asociada con él. Supongamos que estás en un automóvil que viaja hacia el este a 88 metros / segundo cuando se empieza a acelerar el norte a 5,0 metros / segundo2 para 10,0…