Cómo manejar la velocidad como un vector

categoría Educación y lenguas / Ciencia / Física

La velocidad es un vector, y como tal, tiene una magnitud y una dirección asociada con él. Supongamos que estás en un automóvil que viaja hacia el este a 88 metros / segundo cuando se empieza a acelerar el norte a 5,0 metros / segundo2

para 10,0 segundos. ¿Cuál es su velocidad final?

Usted puede pensar que usted puede utilizar esta ecuación para encontrar la respuesta:

vF = vo + la X t

Pero eso no es un vector equation- las cantidades aquí se llaman escalares (la magnitud de un vector es un escalar). Esta es una ecuación escalar, y no es apropiado utilizar aquí porque la aceleración y la velocidad inicial no están en la misma dirección. De hecho, la propia velocidad es un escalar, así que hay que pensar en términos de velocidad, pero no de la velocidad.

Aquí está la misma ecuación como una ecuación vectorial:

vF = vo + la X t

Tenga en cuenta que las velocidades son ahora las velocidades (velocidad es la magnitud de un vector de velocidad) y que todo aquí es un vector excepto el tiempo (que es siempre un escalar). Este cambio significa que la adición se realiza en esta ecuación es la suma de vectores, que es lo que quieres porque vectores pueden manejar además en múltiples dimensiones, no sólo en una línea recta.

Aquí están las ecuaciones de movimiento, escritas como ecuaciones vectoriales:

vF = vo + la X t

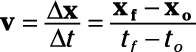
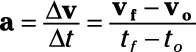
imagen0.jpg image1.jpg image2.jpg

Ejemplo de pregunta

  1. Usted está en un automóvil que viaja hacia el este a 88,0 metros / segundo y luego se acelera hacia el norte a 5,00 metros / segundo2 para 10,0 segundos. ¿Cuál es su velocidad final?

    La respuesta correcta es de 101 metros / segundo.

  1. Comience con esta ecuación vectorial:

    vF = vo + la X t

  2. Esta ecuación es simplemente la suma de vectores, por lo que el tratamiento de las cantidades involucradas como vectores.

    Eso es, vo = (88, 0) metros / segundo y la = (0, 5) metros / segundo2. Esto es lo que la ecuación se parece al conectar los números:

    vF = (88,0, 0) + (0, 5,00) (10,0)

  3. Haz las matematicas:

    vF = (88,0, 0) + (0, 5,00) (10,0) = (88.0, 50.0)

  4. Se le pedirá que encontrar la velocidad final, que es la magnitud de la velocidad. Enchufe sus números en el teorema de Pitágoras.

  5. También puede encontrar la dirección final.

    Aplicar la ecuación de theta = tan-1(y/X) Para encontrar el ángulo, que es tan-1(50,0 / 88,0) = tan-1(0,57) = 29.6 grados en este caso.

Preguntas de práctica

  1. Vas 40,0 metros / segundo al este, y luego acelerar 10,0 metros / segundo2 norte de 10.0 segundos. ¿Cuáles son la dirección y la magnitud de su velocidad final?

  2. Vas 44,0 metros / segundo a 35 grados, y luego acelerar el oeste a 4,0 metros / segundo2 durante 20,0 segundos. ¿Cuáles son la dirección y la magnitud de su velocidad final?

  3. Un disco de hockey va 100,0 metros / segundo a 250 grados cuando es golpeado por un palo de hockey, que lo acelera a 1,0 x 103 metros / segundo2 a los 19 grados durante 0,10 segundos. ¿Cuáles son la dirección y la magnitud de la velocidad final del disco?

  4. Un automóvil se desplaza a lo largo de una carretera helada en 10,0 metros / segundo a 0 grados cuando patines, acelerando a 15 metros / segundo2 a 63 grados para 1,0 segundos. ¿Cuáles son la dirección y la magnitud de la velocidad final del coche?

A continuación se presentan las respuestas a las preguntas de la práctica:

  1. Magnitud 108 metros / segundo, ángulo de 68 grados

  1. Comience con esta ecuación: vF = vo + la X t.

  2. Conecte los números: vF = (40,0, 0) + (0, 10,0) (10,0) = (40,0, 100,0).

  3. Convertir el vector (40.0, 100.0) en forma de magnitud / ángulo. Utilice la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(100.0 / 40.0) = tan-1(2,5) = 68 grados.

  4. Aplicar la ecuación

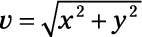
    image3.jpg

    para encontrar la velocidad - la magnitud de la velocidad, que le da 108 metros / segundo.

  • Magnitud 50,7 metros / segundo, ángulo de 150 grados

    1. Comience con esta ecuación: vF = vo + la X t.

    2. Convertir la velocidad original en notación componente vectorial.

      Utilice la ecuación vX = v cos theta para encontrar el X de coordenadas del vector de velocidad original: 44,0 x cos 35 grados = 36,0.

    3. Utilice la ecuación vy = v theta pecado para encontrar la y coordinar de la velocidad: 44,0 x sen 35 grados, o 25.2. Así que la velocidad es (36.0, 25.2) en forma de coordenadas.

    4. Realice la suma de vectores: (36.0, 25.2) + (-4,0, 0) (20,0) = (-44,0, 25,2).

    5. Convertir el vector (-44,0, 25,2) en forma de magnitud / ángulo.

      Utilice la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(25,2 / -44,0) = tan-1(0,57) = 150 grados.

    6. Aplicar la ecuación

      image4.jpg

      para encontrar la velocidad - la magnitud de la velocidad, que le da 50,7 metros / segundo.

    7. Magnitud 86,1 metros / segundo, ángulo de -46 grados

      1. Comience con esta ecuación: vF = vo + la X t.

      2. Convertir la velocidad original en notación componente vectorial.

        Utilice la ecuación vX = v cos theta para encontrar la X coordenadas del vector velocidad inicial: 100,0 x cos 250 grados = -34.2.

      3. Utilice la ecuación vy = v theta pecado para encontrar la y coordinar de la velocidad: 100.0 x sen 250 grados, o -94.0.

        Así que la velocidad original es (-34.2, -94.0) Forma de coordenadas.

      4. Convertir la aceleración en componentes.

        Utilice la ecuación laX = la cos theta para encontrar el X de coordenadas de la aceleración: (1,0 x 103) cos 19 grados = 946.

      5. Utilice la ecuación lay = la theta pecado para encontrar el y de coordenadas de la aceleración: (1,0 x 103) pecar 19 grados, o 325.

        Así que la aceleración es (946, 325) en forma de coordenadas.

      6. Realice la suma de vectores: (-34.2, -94.0) + (945, 325) (0,1) = (60.3, -61.5).

      7. Convertir el vector (60.3, -61.5) en forma de magnitud / ángulo.

      8. Utilice la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(61,5 / 60,3) = tan-1(-1,0) = -46 Grados.

      9. Aplicar la ecuación

        image5.jpg

        para encontrar la velocidad - la magnitud de la velocidad, que le da 86,1 metros / segundo.

      10. Magnitud 21,5 metros / segundo, ángulo de 39 grados

        1. Comience con esta ecuación: vF = vo + la X t.

        2. Convertir la velocidad original al componente notación vectorial: (10.0, 0) metros / segundo.

        3. Convertir la aceleración en componentes. Utilice la ecuación laX = la cos theta para encontrar el X coordenadas de la aceleración: 15 x cos 63 grados = 6.8.

        4. Utilice la ecuación lay = la theta pecado para encontrar el y de coordenadas de la aceleración: 15 x sen 63 grados, o 13.4.

          Así que la aceleración es (6.8, 13.4) en forma de coordenadas.

        5. Realice la suma de vectores: (10.0, 0) + (6,8, 13,4) (1,0) = (16.8, 13.4).

        6. Convertir el vector (16.8, 13.4) en forma de magnitud / ángulo.

          Utilice la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(13,4 / 16,8) = tan-1(0,79) = 39 grados.

        7. Aplicar la ecuación

          image6.jpg

          para encontrar la magnitud de la velocidad, que le da 21,5 metros / segundo.



          8. Artículos Relacionados

          Sobre el autor
          La fuerza es un vector La fuerza es un vector

          Fuerza, como el desplazamiento, velocidad y aceleración, es una cantidad vectorial, que es la razón por la segunda ley de Newton se escribe como sigmaF = ma. Poner en palabras, se dice que la suma vectorial de las fuerzas que actúan sobre un…

          Cómo aceleración centrípeta mantiene un objeto que se mueve en un círculo constante Cómo aceleración centrípeta mantiene un objeto que se mueve en un círculo constante

          En física, cuando un objeto se desplaza en movimiento circular uniforme, su velocidad es constante, lo que significa que la magnitud de la velocidad del objeto no cambia. Por lo tanto, la aceleración no puede tener ningún componente en la misma…

          Cómo la gravedad afecta a la aceleración de un objeto sobre un plano inclinado Cómo la gravedad afecta a la aceleración de un objeto sobre un plano inclinado

          Puede usar la física para determinar cómo la gravedad afecta a la aceleración de un objeto mientras se mueve a lo largo de un plano inclinado. Cuando estás en o cerca de la superficie de la Tierra, la fuerza de la gravedad es constante. Es una…

          Cómo positiva y aceleración negativa se refieren a la velocidad y la velocidad Cómo positiva y aceleración negativa se refieren a la velocidad y la velocidad

          En física, el signo de la aceleración de un objeto depende de su dirección. Si vas más despacio a una parada completa en un coche, por ejemplo, y su velocidad original era positiva y su velocidad final fue de 0, por lo que su aceleración es…

          Cómo agregar vectores juntos Cómo agregar vectores juntos

          Se le pide con frecuencia para añadir vectores en la resolución de problemas de física. Para sumar dos vectores, se colocan la cabeza a la cola y luego encontrar la duración y magnitud del resultado. El orden en que se agregan los dos vectores…

          Cómo calcular la aceleración Cómo calcular la aceleración

          En términos de física, aceleración, la, es la cantidad en la que los cambios de velocidad en una determinada cantidad de tiempo. Teniendo en cuenta las velocidades iniciales y finales, vyo y vF, y los tiempos iniciales y finales sobre las que los…

          Cómo calcular la velocidad de un objeto en función de su desplazamiento Cómo calcular la velocidad de un objeto en función de su desplazamiento

          En la física, la velocidad, que es la tasa de cambio de posición (o la velocidad en una dirección particular), es un vector. Imagine que usted acaba de golpear una bola de tierra en el diamante de béisbol y se está ejecutando a lo largo de la…

          Cómo calcular el tiempo y la distancia de aceleración y la velocidad Cómo calcular el tiempo y la distancia de aceleración y la velocidad

          En una ecuación de la física, dada una aceleración constante y el cambio en la velocidad de un objeto, se puede averiguar tanto el tiempo necesario y la distancia recorrida. Por ejemplo, imagina que eres un auto de carreras. Su aceleración es de…

          Cómo crear un vector Cómo crear un vector

          Un vector es una combinación de exactamente dos valores: una magnitud (como la velocidad de un objeto en movimiento) y una dirección (tal como la dirección de un objeto en movimiento). Todo tipo de cosas se pueden describir con vectores,…

          ¿Cómo encontrar componentes de un vector ¿Cómo encontrar componentes de un vector

          Puede convertir de la manera magnitud / ángulo de la especificación de un vector para la forma de coordenadas de expresión. Si lo hace, es esencial para los tipos de operaciones que puede esperar para ejecutar en vectores, tales como cuando se…

          ¿Cómo encontrar magnitud y dirección de un vector ¿Cómo encontrar magnitud y dirección de un vector

          Si te dan las componentes de un vector, como (3, 4), se puede convertir fácilmente a la forma en magnitud / ángulo de expresar los vectores usando la trigonometría.Por ejemplo, echar un vistazo a el vector en la imagen.Supongamos que te dan las…

          ¿Cómo encontrar componentes del vector ¿Cómo encontrar componentes del vector

          En la física, cuando se rompe un vector en sus partes, las partes se llaman su componentes. Por ejemplo, en el vector (4, 1), el X-eje (horizontal) componente es 4, y el y-(vertical) componente es 1. Por lo general, un problema de física le da un…

          » » » » Cómo manejar la velocidad como un vector