¿Cómo encontrar componentes del vector

En la física, cuando se rompe un vector en sus partes, las partes se llaman su componentes. Por ejemplo, en el vector (4, 1), el X-eje (horizontal) componente es 4, y el y-(vertical) componente es 1. Por lo general, un problema de física le da un ángulo y una magnitud de definir un vector-usted tiene que encontrar los componentes por sí mismo utilizando un poco de trigonometría.

Supongamos que usted sabe que una bola está rodando sobre una mesa plana a 15 grados desde una dirección paralela al borde inferior a una velocidad de 7,0 metros / segundo. Es posible que desee saber cuánto tiempo la pelota se llevará a rodar fuera del metro borde 1,0 a la derecha.

Defina sus ejes para que la pelota está en el origen inicialmente y el X-eje es paralelo al borde inferior de la tabla (véase la figura). Por lo tanto, el problema se descompone para averiguar cuánto tiempo la pelota se llevará a rodar 1,0 metros en el X dirección. Para encontrar el tiempo, primero tiene que saber qué tan rápido la pelota se mueve en la X dirección.

El problema le dice que la pelota está rodando a una velocidad de 7,0 metros / segundo a 15 grados respecto a la horizontal (a lo largo del positivo X-eje), que es un vector: 7,0 metros / segundo a 15 grados le da tanto una magnitud y una dirección. Lo que tenemos aquí es una velocidad - la versión vectorial de la velocidad. La velocidad de la pelota es la magnitud de su vector de velocidad, y cuando se incluye una dirección a esa velocidad, se obtiene el vector de velocidad v.

Para saber qué tan rápido la pelota se desplaza hacia el borde de la mesa, que no necesita la velocidad total de la pelota, pero el X componente de la velocidad de la pelota. los X componente es un escalar (un número, no un vector), y escribir así: v_X. El componente y de vector de velocidad de la pelota es v_y. Por lo tanto, se puede decir que

v = (v_X, v_y)

Así es como te expresas romper un vector en sus componentes. ¿Cuál es v_X ¿Aquí? Y para el caso, lo que es v_y, el y componente de la velocidad? El vector tiene una longitud (7,0 metros / segundo) y una dirección

Y usted sabe que el borde de la mesa es de 1,0 metros a la derecha.

Como se puede ver en la figura, hay que usar un poco de trigonometría para resolver este vector en sus componentes. Sin sudar. La trigonometría es fácil después de llegar hasta los ángulos que se ven en la figura.

La magnitud de un vector v se expresa como v, y en la figura, se puede ver que la siguiente es cierto:

Las dos ecuaciones vectoriales componente son vale la pena conocer, porque se les ve mucho en cualquier curso de física comenzando. Asegúrese de saber cómo funcionan, y siempre ellos tienen a su alcance.

Por supuesto, si usted se olvida de estas ecuaciones, siempre puedes descargarlos desde la trigonometría básica. Usted puede recordar que el seno y el coseno de un ángulo en un triángulo rectángulo se define como la relación entre el lado opuesto y el lado adyacente a la hipotenusa, así:

Multiplicando ambos lados de estas ecuaciones v, se puede expresar la X y y componentes del vector como

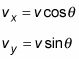
Usted puede ir más allá, relacionando cada lado del triángulo a cada otro lado (y si usted sabe que

puede derivar todo esto de las dos ecuaciones anteriores según sea preciso sin necesidad de memorizar todos estos):

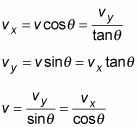
Tu sabes

para que pueda encontrar el X componente de la velocidad de la pelota, v_X, de esta manera:

La conexión de los números que da

Ahora ya sabe que la pelota se desplaza a 6,8 metros / segundo a la derecha. Y porque usted también sabe que el borde de la mesa es de 1,0 metro de distancia, se puede dividir la distancia por la velocidad para obtener el tiempo:

Porque usted sabe qué tan rápido va la pelota en el X dirección, ahora se sabe la respuesta al problema: La pelota se llevará a 0.15 segundos de caer por el borde de la mesa. Qué tal el y componente de la velocidad? Eso es fácil de encontrar, también: