La fuerza es un vector

categoría Educación y lenguas / Ciencia / Física

Fuerza, como el desplazamiento, velocidad y aceleración, es una cantidad vectorial, que es la razón por la segunda ley de Newton se escribe como sigmaF

= ma. Poner en palabras, se dice que la suma vectorial de las fuerzas que actúan sobre un objeto es igual a su masa (un escalar) multiplicada por su aceleración (un vector).

Debido a la fuerza es una magnitud vectorial, agrega fuerzas juntos como vectores. Eso encaja a la derecha en la segunda ley de Newton.

Ejemplo de pregunta

  1. Suponga que tiene dos fuerzas como se muestra: LA = 5,0 N a 40 grados, y B = 7,0 N a 125 grados. ¿Cuál es la fuerza neta, sigmaF?

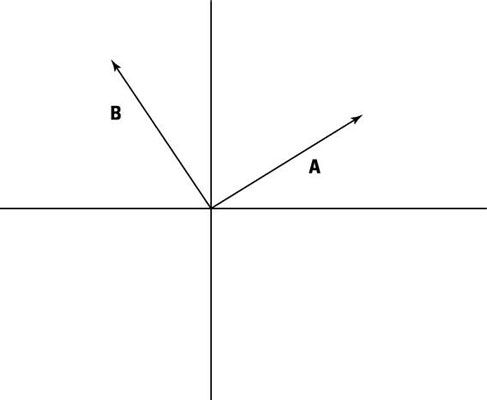
    imagen0.jpg

    La respuesta correcta es la magnitud 8,9 N, el ángulo de 91 grados.

  1. Convertir vigor LA a notación componente vectorial. Utilice la ecuación LAX = LA cos theta para encontrar el X coordinar de la fuerza: 5.0 cos 40 grados = 3.8.

  2. Utilice la ecuación LAy = LA theta pecado para encontrar el y coordinar de la fuerza: 5.0 pecado 40 grados, o 3.2. Eso hace que el vector LA (3.8, 3.2) en forma de coordenadas.

  3. Convertir el vector B en componentes. Utilice la ecuación BX = B cos theta para encontrar el X coordenadas de la aceleración: 7,0 cos 125 grados = -4.0.

  4. Utilice la ecuación By = B theta pecado para encontrar el y coordenadas de la segunda fuerza: 7.0 pecado 125 grados, o 5.7. Eso hace la fuerza B (-4.0, 5.7) en forma de coordenadas.

  5. Realice la suma de vectores para encontrar la fuerza neta: (3.8, 3.2) + (-4,0, 5,7) = (-0.2, 8.9).

  6. Convertir el vector (-0.2, 8.9) en forma de magnitud / ángulo. Utilice la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(-44,5) = 91 grados.

  7. Aplicar la ecuación

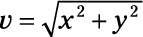
    image1.jpg

    para encontrar la magnitud de la fuerza neta, que le da 8,9 N.

Preguntas de práctica

  1. Añadir dos fuerzas: A es 8,0 N a 53 grados, y B es 9,0 N a 19 grados.

  2. Añadir dos fuerzas: A es 16,0 N a 39 grados, y B es 5,0 N a 125 grados.

  3. Añadir dos fuerzas: A es 22,0 N a 68 grados, y B es 6,0 N a los 24 grados.

  4. Añadir dos fuerzas: A es 12,0 N a 129 grados, y B es 3,0 N a 225 grados.

A continuación se presentan las respuestas a las preguntas de la práctica:

  1. Magnitud: 16 N- Ángulo: 35 grados

  1. Convertir vigor LA a notación componente vectorial. Utilice la ecuación LAX = LA cos theta para encontrar el X coordinar de la fuerza LA: 8.0 cos 53 grados = 4,8 N.

  2. Utilice la ecuación LAy = LA theta pecado para encontrar el y coordinar de la fuerza LA: 8.0 pecado 53 grados = 6,4 N. Eso hace la fuerza LA (4.8, 6.4) N en forma de coordenadas.

  3. Convertir el vector B en componentes. Utilice la ecuación BX = B cos theta para encontrar el X coordinar de la fuerza B: 9.0 cos 19 grados = 8,5 N.

  4. Utilice la ecuación By = B theta pecado para encontrar el y coordenada de la segunda fuerza: 9.0 pecado 19 grados = 2,9 N. Eso hace la fuerza B (8.5, 2.9) N en forma de coordenadas.

  5. Realizar la suma de vectores para encontrar la fuerza neta: (4.8, 6.4) N + (8.5, 2.9) N = (13.3, 9.3) N.

  6. Convertir el vector de fuerza (13.3, 9.3) N en magnitud formulario / ángulo. Utilice la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(0,70) = 35 grados.

  7. Aplicar la ecuación

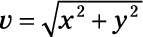
    image2.jpg

    para encontrar la magnitud de la fuerza neta, que le da 16 N.

  • Magnitud: 17 N- Ángulo: 56 grados

    1. Convertir vigor LA a notación componente vectorial. Utilice la ecuación LAX = LA cos theta para encontrar el X coordinar de la fuerza LA: 16.0 cos 39 grados = 12.4 N.

    2. Utilice la ecuación LAy = LA theta pecado para encontrar el y coordinar de la fuerza LA: 16.0 pecado 39 grados = 10.0 N. Eso hace la fuerza LA (12.4, 10.0) N en forma de coordenadas.

    3. Convertir vigor B en componentes. Utilice la ecuación BX = B cos theta para encontrar el X coordinar de la fuerza B: 5.0 cos 125 grados = -2,9 N.

    4. Utilice la ecuación By = B theta pecado para encontrar la y coordenada de la segunda fuerza: 5.0 pecado 125 grados = 4,1 N. Eso hace la fuerza B (-2,9, 4,1) N en forma de coordenadas.

    5. Realizar la suma de vectores para encontrar la fuerza neta: (12.4, 10.0) N + (-2,9, 4,1) N = (9,5, 14,1) N.

    6. Convertir el vector de fuerza (9.5, 14.1) N en magnitud formulario / ángulo. Utilice la ecuación de theta = tan-1 (y/X) Para encontrar el ángulo: tan-1(1,5) = 56 grados.

    7. Aplicar la ecuación

      image3.jpg

      para encontrar la magnitud de la fuerza neta, que le da 17 N.

    8. Magnitud: 27 N- Ángulo: 59 grados

      1. Convertir vigor LA a notación componente vectorial. Utilice la ecuación LAX = LA cos theta para encontrar el X coordinar de la fuerza LA: 22.0 cos 68 grados = 8.24N.

      2. Utilice la ecuación LAy = LA theta pecado para encontrar la y coordinar de la fuerza LA: 22.0 pecado 68 grados = 20.4 N. Eso hace la fuerza LA (8.24, 20.4) N en forma de coordenadas.

      3. Convertir vigor B en componentes. Utilice la ecuación BX = B cos theta para encontrar la X coordinar de la fuerza B: 6.0 cos 24 grados = 5,5 N.

      4. Utilice la ecuación By = B theta pecado para encontrar la y coordinar de la fuerza B: 6.0 pecado 24 grados = 2,4 N. Eso hace la fuerza B (5.5, 2.4) N en forma de coordenadas.

      5. Realizar la suma de vectores para encontrar la fuerza neta: (8.24, 20.3) N + (5.5, 2.4) N = (13.7, 22.7) N.

      6. Convertir el vector de fuerza (13.7, 22.7) N en magnitud formulario / ángulo. Utilice la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(1,66) = 59 grados.

      7. Aplicar la ecuación

        image4.jpg

        para encontrar la magnitud de la fuerza neta, que le da 27 N.

      8. Magnitud: 12 N- Ángulo: 143 grados

        1. Convertir vigor LA a notación componente vectorial. Utilice la ecuación LAX = LA cos theta para encontrar el X coordinar de la fuerza LA: 12.0 cos 129 grados = -7.6.

        2. Utilice la ecuación LAy = LA theta pecado para encontrar la y coordinar de la fuerza LA: 12.0 pecado 129 grados = 9,3 N. Eso hace la fuerza LA (-7,6, 9,3) N en forma de coordenadas.

        3. Convertir vigor B en componentes. Utilice la ecuación BX = B cos theta para encontrar la X coordinar de la fuerza B: 3.0 cos 225 grados = -2,1 N.

        4. Utilice la ecuación By = B theta pecado para encontrar la y coordinar de la fuerza B: 3.0 pecado 225 grados = N. -2,1 Eso hace la fuerza B (-2,1, -2,1) N en forma de coordenadas.

        5. Realizar la suma de vectores para encontrar la fuerza neta: (-7.6, 9.3) N + (-2,1, -2,1) N = (-9,7, 7,2) N.

        6. Convertir el vector de fuerza (-9,7, 7,2) N en magnitud formulario / ángulo. Utilice la ecuación de theta = tan-1(y/X) Para encontrar el ángulo: tan-1(-0,74) = 143 grados.

        7. Aplicar la ecuación

          image5.jpg

          para encontrar la magnitud de la fuerza neta, que le da 12 N.



          8. Artículos Relacionados

          Sobre el autor
          Cálculo de la fuerza neta y aceleración Cálculo de la fuerza neta y aceleración

          Newton dice sigmaF = mla, lo que significa que agrega todos los vectores de fuerza en conjunto para obtener la fuerza neta. Eso es lo que por lo general funciona cuando se tiene que averiguar F = mamá problemas de la física. A menudo, una serie de…

          Colisiones en dos dimensiones Colisiones en dos dimensiones

          Las colisiones pueden tener lugar en dos dimensiones. Por ejemplo, pelotas de fútbol pueden pasar de cualquier manera en un campo de fútbol, ​​no sólo a lo largo de una sola línea. Balones de fútbol puede llegar a ir al norte o al sur, al…

          La conversión entre ángulos La conversión entre ángulos

          Estudio en física por lo general comienza con movimiento lineal, que es el movimiento en línea recta. Gran parte de la física se centra en el movimiento angular, sin embargo, que es el movimiento de los objetos en los alrededores de círculos o…

          Hacer frente a la fuerza neta Hacer frente a la fuerza neta

          Hay a menudo más de una fuerza involucrada cuando se está arrastrando una masa sobre una distancia. Basta pensar en las fuerzas de la fricción y la gravedad de un objeto sobre un plano inclinado. Por ejemplo, echar un vistazo a la figura, donde…

          Encontrar la fuerza de la gravedad a lo largo de un plano inclinado Encontrar la fuerza de la gravedad a lo largo de un plano inclinado

          Puede usar la física para determinar la fuerza de la gravedad sobre un objeto que se mueve a lo largo de un plano inclinado. Puede romper el peso del objeto en componentes que son paralelas a y perpendicular al plano. El componente perpendicular al…

          Cómo agregar vectores juntos Cómo agregar vectores juntos

          Se le pide con frecuencia para añadir vectores en la resolución de problemas de física. Para sumar dos vectores, se colocan la cabeza a la cola y luego encontrar la duración y magnitud del resultado. El orden en que se agregan los dos vectores…

          Cómo calcular el trabajo en base a la fuerza aplicada en un ángulo Cómo calcular el trabajo en base a la fuerza aplicada en un ángulo

          Si se aplica la fuerza en un ángulo en lugar de paralelo a la dirección del movimiento, tiene que suministrar más fuerza para realizar la misma cantidad de trabajo. Puede usar la física para calcular la cantidad de trabajo que se requiere, por…

          ¿Cómo encontrar componentes de un vector ¿Cómo encontrar componentes de un vector

          Puede convertir de la manera magnitud / ángulo de la especificación de un vector para la forma de coordenadas de expresión. Si lo hace, es esencial para los tipos de operaciones que puede esperar para ejecutar en vectores, tales como cuando se…

          ¿Cómo encontrar magnitud y dirección de un vector ¿Cómo encontrar magnitud y dirección de un vector

          Si te dan las componentes de un vector, como (3, 4), se puede convertir fácilmente a la forma en magnitud / ángulo de expresar los vectores usando la trigonometría.Por ejemplo, echar un vistazo a el vector en la imagen.Supongamos que te dan las…

          Cómo manejar la velocidad como un vector Cómo manejar la velocidad como un vector

          La velocidad es un vector, y como tal, tiene una magnitud y una dirección asociada con él. Supongamos que estás en un automóvil que viaja hacia el este a 88 metros / segundo cuando se empieza a acelerar el norte a 5,0 metros / segundo2 para 10,0…

          Fuerza de medición y la dirección mediante la suma de vectores Fuerza de medición y la dirección mediante la suma de vectores

          En física, tomar ángulos (o dirección) en cuenta en la medición de la fuerza, que tiene que hacer un poco de la suma de vectores. Echa un vistazo a la siguiente figura. En este caso, la masa m no se está moviendo, y ya está aplicando una…

          La segunda ley de Newton: la forma neta fuerza, masa y aceleración afectan el movimiento La segunda ley de Newton: la forma neta fuerza, masa y aceleración afectan el movimiento

          Primera ley de Newton dice que un objeto permanece en movimiento uniforme a menos que actúe por una fuerza neta. Cuando se aplica una fuerza neta, el objeto se acelera. La segunda ley de Newton se detalla la relación entre la fuerza neta, la masa…

          » » » » La fuerza es un vector