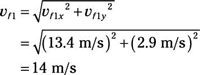Colisiones en dos dimensiones

categoría Educación y lenguas / Ciencia / Física

Las colisiones pueden tener lugar en dos dimensiones. Por ejemplo, pelotas de fútbol pueden pasar de cualquier manera en un campo de fútbol, ​​no sólo a lo largo de una sola línea. Balones de fútbol puede llegar a ir al norte o al sur, al este o al oeste, o una combinación de ellos. Así que hay que estar preparado para manejar colisiones en dos dimensiones.

Ejemplo de pregunta

  1. En la figura, se ha producido un accidente en un restaurante italiano, y dos albóndigas están chocando. Asumiendo que vo1 = 10,0 m / s, vo2 = 5,0 m / s, vF2 = 6,0 m / s, y las masas de las albóndigas son iguales, ¿cuáles son theta y vF1?

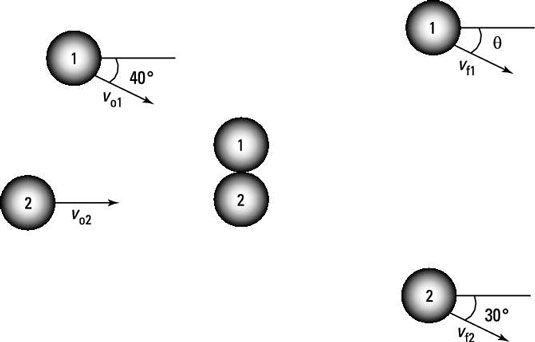
    imagen0.jpg

    La respuesta correcta es theta = 24 grados y vF1 = 8,2 m / s.

  1. No se puede asumir que estas albóndigas conservar la energía cinética cuando chocan porque las albóndigas probablemente se deforman de la colisión. Sin embargo, el ímpetu se conserva. De hecho, el impulso se conserva tanto en el X y y direcciones, lo que significa

    pfx = pbuey

    y

    pfy = poy

  2. Esto es lo que el impulso original en el X dirección fue:

    pfx = pbuey = m1vo1 cos 40 grados + m2vo2

  3. Momentum se conserva en el X dirección, por lo que obtener

    pfx = pbuey = m1vo1 cos 40 grados + m2vo2 = m1vF1X + m2vF2 cos 30 grados

  4. Lo que significa que

    m1vF1X = m1vo1 cos 40 grados + m2vo2 - m2vF2 cos 30 grados

  5. Dividido por m1:

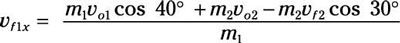
    image1.jpg

    Y por eso m1 = m2, esto se convierte

    vF1X = vo1 cos 40 grados + vo2 - vF2 cos 30 grados

  6. Conecte los números:

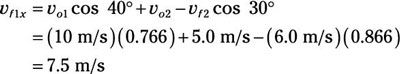
    image2.jpg

  7. Ahora, para el y dirección. Esto es lo que el impulso original en el y dirección parece (en la dirección hacia abajo):

    pfy = poy = m1vo1 pecar 40 grados

  8. Establecer que igual al momento final en el y dirección:

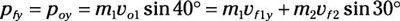
    image3.jpg

  9. Esa ecuación se convierte en:

    m1vF1y = m1vo1 pecar de 40 grados - m2vF2 pecar 30 grados

  10. Resolver para el componente de velocidad final de albóndigas de 1 y velocidad:

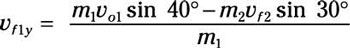
    image4.jpg

  11. Debido a que las dos masas son iguales, esto se convierte

    vF1y = vo1 pecar de 40 grados - vF2 pecar 30 grados

  12. Conecte los números:

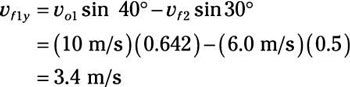
    image5.jpg

  13. Por lo tanto:

    vF1X = 7,5 m / s (a la derecha)vF1y = 3.4 m / s (hacia abajo)

    Eso significa que el ángulo theta es

    image6.jpg

    Y la magnitud de vF1 es

    image7.jpg

Preguntas de práctica

  1. Suponga que los dos objetos en la figura anterior son discos de hockey de igual masa. Asumiendo que vo1 = 15 m / s, vo2 = 7,0 m / s, y vF2 = 7,0 m / s, ¿cuáles son theta y vF1, suponiendo que el impulso se conserva pero la energía cinética no lo es?

  2. Suponga que los dos objetos en la figura siguiente son las pelotas de tenis de igual masa. Asumiendo que vo1 = 12 m / s, vo2 = 8,0 m / s, y vF2 = 6,0 m / s, ¿cuáles son theta y vF1, suponiendo que el impulso se conserva pero la energía cinética no lo es?

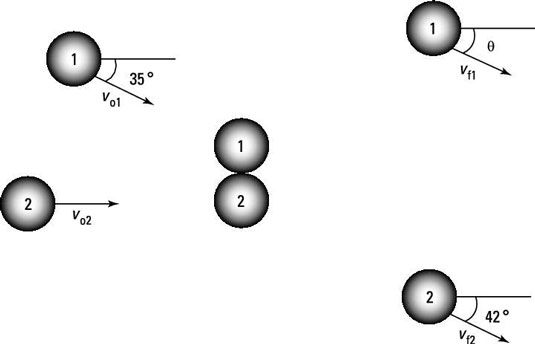
    image8.jpg

A continuación se presentan las respuestas a las preguntas de la práctica:

  1. 14 m / s, 26 grados

  1. Momentum se conserva en esta colisión. De hecho, el impulso se conserva tanto en el X y y direcciones, lo que significa los siguientes son verdaderas:

    pfx = pbueypfy = poy

  2. El impulso original en el X dirección fue

    pfx = pbuey = m1vo1 cos 40 grados + m2vo2

  3. Momentum se conserva en el X dirección, por lo

    pfx = pbuey = m1vo1 cos 40 grados + m2vo2 = m1vF1X + m2vF2 cos 30 grados

  4. La solución para m1vF1X te dio:

    m1vF1X = m1vo1 cos 40 grados + m2vo2 - m2vF2 cos 30 grados

  5. Dividido por m1:

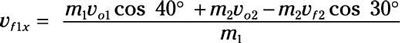
    imagen9.jpg

    Porque m1 = m2, que la ecuación se convierte en

    vF1X = vo1 cos 40 grados + vo2 - vF2 cos 30 grados

  6. Conecte los números:

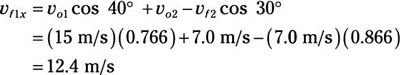
    image10.jpg

  7. Ahora, para el y dirección. El impulso original en el y dirección fue

    pfy = poy = m1vo1 pecar 40 grados

  8. Establecer que igual al momento final en el y dirección:

    pfy = poy = m1vo1 pecar 40 grados = m1vF1y + m2vF2 pecar 30 grados

  9. Que se convierte en

    m1vF1y = m1vo1 pecar de 40 grados - m2vF2 pecar 30 grados

  10. Resuelva para la componente de la velocidad final del duende malicioso de 1 y velocidad:

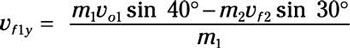
    image11.jpg

  11. Debido a que las dos masas son iguales, la ecuación se convierte

    vF1y = vo1 pecar de 40 grados - vF2 pecar 30 grados

  12. Conecte los números:

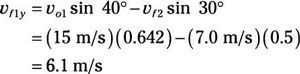
    image12.jpg

  13. Así

    vF1X = 12,4 m / svF1y = 6.1 m / s

    Eso significa que el ángulo theta es

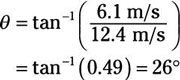
    image13.jpg

    Y la magnitud de vf1 es

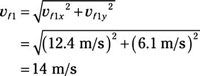
    image14.jpg

  • 14 m / s, 12 grados

    1. En esta situación, el impulso se conserva tanto en el X y y direcciones, por lo que el siguiente es cierto:

      pfx = pbueypfy = poy

    2. El impulso original en el X dirección fue

      pfx = pbuey = m1vo1 cos 35 grados + m2vo2

    3. Momentum se conserva en el X dirección, así:

      pfx = pbuey = m1vo1 cos 35 grados + m2vo2 = m1vF1X + m2vF2 cos 42 grados

    4. Lo que significa:

      m1vF1X = m1vo1 cos 35 grados + m2vo2 - m2vF2 cos 42 grados

    5. Dividido por m1:

      image15.jpg

      Porque m1 = m2, esto se convierte

      vF1X = vo1 cos 35 grados + vo2 - vF2 cos 42 grados

    6. Conecte los números:

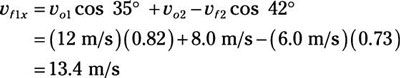
      image16.jpg

    7. Ahora, para el y dirección. El impulso original en el y dirección fue

      pfy = poy = m1vo1 pecar 35 grados

    8. Establecer que igual al momento final en el y dirección:

      pfy = poy = m1vo1 pecar 35 grados = m1vF1y + m2vF2 pecar 42 grados

      La solución para m1vF1y te dio:

      m1vF1y = m1vo1 pecar 35 grados - m2vF2 pecar 42 grados

    9. Resuelva para la componente de la velocidad final del duende malicioso de 1 y velocidad:

      image17.jpg

    10. Debido a que las dos masas son iguales, la ecuación se convierte

      vF1y = vo1 pecar 35 grados - vF2 pecar 42 grados

    11. Conecte los números:

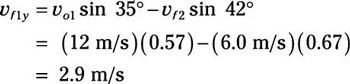
      image18.jpg

    12. Por lo tanto:

      vF1X = 13,4 m / svF1y = 2,9 m / s

      Lo que significa que el ángulo theta es

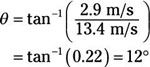
      image19.jpg

      Y la magnitud de vF1 es

      image20.jpg


      13. Artículos Relacionados

      Sobre el autor
      La conservación de la energía cinética La conservación de la energía cinética

      En algunos tipos de colisiones, llamado colisiones elásticas, la energía cinética y el momento se conservan. ¿Cómo son las colisiones elásticas como? En general, no hay deformación permanente de cualquiera de los objetos de una colisión…

      La conversión entre ángulos La conversión entre ángulos

      Estudio en física por lo general comienza con movimiento lineal, que es el movimiento en línea recta. Gran parte de la física se centra en el movimiento angular, sin embargo, que es el movimiento de los objetos en los alrededores de círculos o…

      La fuerza es un vector La fuerza es un vector

      Fuerza, como el desplazamiento, velocidad y aceleración, es una cantidad vectorial, que es la razón por la segunda ley de Newton se escribe como sigmaF = ma. Poner en palabras, se dice que la suma vectorial de las fuerzas que actúan sobre un…

      Cómo agregar vectores juntos Cómo agregar vectores juntos

      Se le pide con frecuencia para añadir vectores en la resolución de problemas de física. Para sumar dos vectores, se colocan la cabeza a la cola y luego encontrar la duración y magnitud del resultado. El orden en que se agregan los dos vectores…

      Cómo calcular las velocidades de dos objetos con diferentes masas después de una colisión elástica Cómo calcular las velocidades de dos objetos con diferentes masas después de una colisión elástica

      Cuando una colisión entre dos objetos es elástica, la energía cinética se conserva. En física, la forma más básica de mirar colisiones elásticas es examinar cómo las colisiones funcionan a lo largo de una línea recta. Si ejecuta su auto de…

      Cómo crear un vector Cómo crear un vector

      Un vector es una combinación de exactamente dos valores: una magnitud (como la velocidad de un objeto en movimiento) y una dirección (tal como la dirección de un objeto en movimiento). Todo tipo de cosas se pueden describir con vectores,…

      ¿Cómo encontrar componentes de un vector ¿Cómo encontrar componentes de un vector

      Puede convertir de la manera magnitud / ángulo de la especificación de un vector para la forma de coordenadas de expresión. Si lo hace, es esencial para los tipos de operaciones que puede esperar para ejecutar en vectores, tales como cuando se…

      ¿Cómo encontrar magnitud y dirección de un vector ¿Cómo encontrar magnitud y dirección de un vector

      Si te dan las componentes de un vector, como (3, 4), se puede convertir fácilmente a la forma en magnitud / ángulo de expresar los vectores usando la trigonometría.Por ejemplo, echar un vistazo a el vector en la imagen.Supongamos que te dan las…

      ¿Cómo encontrar la velocidad de dos objetos después de la colisión ¿Cómo encontrar la velocidad de dos objetos después de la colisión

      Usted puede utilizar el principio de conservación del momento para medir las características de movimiento, tales como la velocidad. Digamos, por ejemplo, que estás en una expedición de la física y le toca pasar por un lago congelado en un…

      Cómo manejar la velocidad como un vector Cómo manejar la velocidad como un vector

      La velocidad es un vector, y como tal, tiene una magnitud y una dirección asociada con él. Supongamos que estás en un automóvil que viaja hacia el este a 88 metros / segundo cuando se empieza a acelerar el norte a 5,0 metros / segundo2 para 10,0…

      Fuerza de medición y la dirección mediante la suma de vectores Fuerza de medición y la dirección mediante la suma de vectores

      En física, tomar ángulos (o dirección) en cuenta en la medición de la fuerza, que tiene que hacer un poco de la suma de vectores. Echa un vistazo a la siguiente figura. En este caso, la masa m no se está moviendo, y ya está aplicando una…

      Momentum en la física Momentum en la física

      Momentum es la cantidad más importante cuando se trata de manejar las colisiones en la física. Momentum es una cantidad física definida como el producto de la masa multiplicada por la velocidad. Tenga en cuenta la definición dice la velocidad,…

      » » » » Colisiones en dos dimensiones