La conservación de momentum

categoría Educación y lenguas / Ciencia / Física

La principal herramienta que tiene en el cálculo de lo que va a pasar en las colisiones es el conocimiento de que el momento se conserva. Usted sabe que el momento total antes de la colisión es la misma que la cantidad de movimiento total después de la colisión, siempre y cuando no hay fuerzas externas significativas.

Cuando tienes dos objetos que chocan (uno es inicialmente en reposo y el otro se mueve), y usted sabe la velocidad final y la masa de un objeto después de la colisión, se puede calcular la velocidad final del otro objeto. Usted puede hacer esto debido a que la cantidad de movimiento total se conserva, por lo que es lo mismo, antes y después de la colisión, como se muestra por esta ecuación:

po = pF

Ejemplo de pregunta

  1. Una bola de billar con una masa de 170 gy una velocidad de 30 m / s golpea otra pelota piscina que está en reposo. Si la primera bola de billar termina yendo en la misma dirección con una velocidad de 10 m / s, ¿cuál es la nueva velocidad de la segunda bola de billar?

    La respuesta correcta es 20 m / s.

  1. Utilice la ecuación po P =F.

  2. Todos los viajes se encuentra en la misma dirección en esta pregunta, así que usted puede tratarlo como una ecuación escalar. Encontrar el momento total originales:

    po = (0,17 kg) (30 m / s) = 5,1 kg-m / s

  3. El momento total inicial es igual al impulso final total, que viene dada por esta expresión, en donde p2f es el momento final de la segunda bola:

    po = 5,1 kg-m / s = pF = (0,17 kg) (10 m / s) + p2f

  4. Resolver p2f:

    p2f = 5,1 kg-m / s - 1,7 kg-m / s = 3,4 kg-m / s

  5. Dividir p2f por la masa de la bola de billar para encontrar su velocidad:

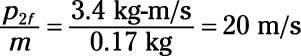
    imagen0.jpg

Preguntas de práctica

  1. A 160-g disco de hockey que viaja a 60 m / s golpea un disco estacionario. Si el primer disco termina yendo a los 20 m / s en la misma dirección que el segundo disco, qué tan rápido se está moviendo el segundo disco?

  2. Usted está conduciendo un auto de choque en un circo parque de diversiones a los 18 m / s, y golpear a otro coche que está en reposo.

    Si usted termina yendo a 6,0 m / s, ¿cuál es la velocidad final del otro coche, ya que ambos coches tienen masa 100,0 kg, tiene masa 80,0 kg, y la otra persona tiene una masa de 70,0 kg?

  3. 3.En el campo deportivo, una pelota de golf con una masa de 0.20 kg y la velocidad de 100,0 m / s golpea un balón de fútbol en reposo que tiene una masa de 0,45 kg.

    Si la pelota de golf termina en reposo, lo que es velocidad final de la pelota de fútbol, ​​ya que viaja en la misma dirección que la pelota de golf viajaba originalmente?

  4. Estás parado en un semáforo cuando un coche 1.000,0 kg (incluido el conductor) te golpea por la espalda a 10,0 m / s. Ouch.

    Si el otro coche termina moviéndose a 6 m / s, y si usted y su automóvil tiene una masa de 940 kg, lo que es su velocidad final?

A continuación se presentan las respuestas a las preguntas de la práctica:

  1. 58 m / s

  1. Utilice la ecuación po P =F.

  2. Los discos se desplazan en la misma dirección que aquí, por lo que puede tratar esto como una ecuación escalar. Encontrar el momento total originales:

    po = (0,16 kg) (60 m / s) = 9,6 kg-m / s

  3. Este es igual al momento final total, que viene dada por esta expresión, donde p2F es el impulso final del segundo disco:

    po = 9,6 kg-m / s = pF = (0,16 kg) (20 m / s) + p2F

  4. Resolver p2F:

    p2F = 9,6 kg-m / s - 0,32 kg-m / s = 9,28 kg-m / s

  5. 5.Dividir p2F en masa de la pastilla para encontrar su velocidad:

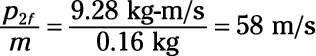
    image1.jpg

  • 13 m / s

    1. Use la ecuación po P =F.

    2. Los coches de choque viajan en la misma dirección que aquí, por lo que puede tratar esto como una ecuación escalar. Encontrar el momento total originales:

      po = (18 m / s) (100,0 kg + 80,0 kg) = 3.240 kg-m / s

    3. Este es igual al momento final total, que viene dada por esta expresión, donde p2F es el impulso final del segundo auto de choque:

      po = 3.240 kg-m / s = pF = (100,0 kg + 80,0 kg) (6,0 m / s) + p2F

    4. Resolver p2F:

      p2F = 3.240 kg-m / s - 1,080 kg-m / s = 2,160 kg-m / s

    5. Dividir p2F por el auto de choque y la masa de la persona para encontrar su velocidad:

      image2.jpg

      que se redondea a 13 con cifras significativas

    6. 44 m / s

      1. Utilice la ecuación po = pF.

      2. Encontrar el momento total originales:

        po = (0,20 kg) (100,0 m / s) = 20 kg-m / s

      3. Este es igual al momento final total, que viene dada por esta expresión, donde p2F es el impulso definitivo de la pelota de fútbol:

        po = 20 kg-m / s = pF = p2F

      4. Resolver p2F:

        p2F = 20 kg-m / s

      5. Dividir p2F en masa de la pelota de fútbol para encontrar su velocidad:

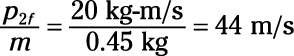
        image3.jpg

      6. 4.2 m / s

        1. Utilice la ecuación po = pF.

        2. Encontrar el momento total originales:

          po = (1.000,0 kg) (10,0 m / s) = 10.000 kg-m / s

        3. Este es igual al momento final total, que viene dada por la siguiente expresión, donde p2F es el impulso final del coche:

          po = 10.000 kg-m / s = pF = (1.000,0 kg) (6 m / s) + p2F

        4. Resolver p2F:

          p2F = 4,000 kg-m / s

        5. Dividir p2F por usted y la masa de su coche para encontrar su velocidad:

          image4.jpg


          6. Artículos Relacionados

          Sobre el autor
          Cómo positiva y aceleración negativa se refieren a la velocidad y la velocidad Cómo positiva y aceleración negativa se refieren a la velocidad y la velocidad

          En física, el signo de la aceleración de un objeto depende de su dirección. Si vas más despacio a una parada completa en un coche, por ejemplo, y su velocidad original era positiva y su velocidad final fue de 0, por lo que su aceleración es…

          Cómo el principio de conservación de las obras de impulso Cómo el principio de conservación de las obras de impulso

          En física, el principio de conservación del momento establece que cuando se tiene un sistema aislado, sin fuerzas externas, el momento total inicial de los objetos antes de una colisión es igual a la cantidad de movimiento total final de los…

          Cómo calcular el momento angular Cómo calcular el momento angular

          En física, se puede calcular el momento angular de la misma manera que se calcula la cantidad de movimiento - sólo momento sustituto de inercia de la masa, y la velocidad angular de la velocidad.Imagínate a un niño pequeño en un paseo patio…

          Cómo calcular la fuerza de impulso y el impulso Cómo calcular la fuerza de impulso y el impulso

          En física, se puede utilizar el teorema de impulso-momento de calcular la fuerza basada en el impulso y el impulso. Por ejemplo, se puede relacionar el impulso con que se golpea un objeto para su consiguiente cambio en el momento. De acuerdo con el…

          Cómo calcular la energía cinética de un objeto Cómo calcular la energía cinética de un objeto

          Puede usar la física para calcular la energía cinética de un objeto. Cuando empiece a empujar o tirar de un objeto fijo con una fuerza constante, empieza a mover si la fuerza que se ejerce es mayor que las fuerzas netas que resisten el…

          Cómo calcular el momento de inercia de diferentes formas y sólidos Cómo calcular el momento de inercia de diferentes formas y sólidos

          En la física, cuando se calcula momento de un objeto de la inercia, debe tener en cuenta no sólo la masa del objeto, sino también cómo se distribuye la masa. Por ejemplo, si dos discos tienen la misma masa, pero uno tiene toda la masa alrededor…

          Cómo calcular el tiempo y la distancia de aceleración y la velocidad Cómo calcular el tiempo y la distancia de aceleración y la velocidad

          En una ecuación de la física, dada una aceleración constante y el cambio en la velocidad de un objeto, se puede averiguar tanto el tiempo necesario y la distancia recorrida. Por ejemplo, imagina que eres un auto de carreras. Su aceleración es de…

          Cómo calcular las velocidades de dos objetos con diferentes masas después de una colisión elástica Cómo calcular las velocidades de dos objetos con diferentes masas después de una colisión elástica

          Cuando una colisión entre dos objetos es elástica, la energía cinética se conserva. En física, la forma más básica de mirar colisiones elásticas es examinar cómo las colisiones funcionan a lo largo de una línea recta. Si ejecuta su auto de…

          ¿Cómo encontrar la velocidad de dos objetos después de la colisión ¿Cómo encontrar la velocidad de dos objetos después de la colisión

          Usted puede utilizar el principio de conservación del momento para medir las características de movimiento, tales como la velocidad. Digamos, por ejemplo, que estás en una expedición de la física y le toca pasar por un lago congelado en un…

          ¿Cómo encontrar la velocidad de un objeto antes de la colisión ¿Cómo encontrar la velocidad de un objeto antes de la colisión

          En física, el principio de conservación del momento es muy útil cuando no se puede medir la velocidad con un simple cronómetro. Digamos, por ejemplo, que acepta un trabajo de consultoría de un fabricante de municiones que quiere medir la…

          Cómo manejar la velocidad como un vector Cómo manejar la velocidad como un vector

          La velocidad es un vector, y como tal, tiene una magnitud y una dirección asociada con él. Supongamos que estás en un automóvil que viaja hacia el este a 88 metros / segundo cuando se empieza a acelerar el norte a 5,0 metros / segundo2 para 10,0…

          Momentum en la física Momentum en la física

          Momentum es la cantidad más importante cuando se trata de manejar las colisiones en la física. Momentum es una cantidad física definida como el producto de la masa multiplicada por la velocidad. Tenga en cuenta la definición dice la velocidad,…

          » » » » La conservación de momentum