Cómo calcular el momento angular

En física, se puede calcular el momento angular de la misma manera que se calcula la cantidad de movimiento - sólo momento sustituto de inercia de la masa, y la velocidad angular de la velocidad.

Imagínate a un niño pequeño en un paseo patio girar, como un merry-go-round, y ella está gritando que quiere bajar. Tienes que dejar el paseo de giro, pero va a tomar un poco de esfuerzo. ¿Por qué? Debido a que tiene momento angular.

Momento lineal, p, se define como el producto de la masa y la velocidad:

p = mv

Esta es una cantidad que se conserva cuando no hay fuerzas externas que actúan. Cuanto más masiva y más rápido mover un objeto, mayor es la magnitud de impulso.

Física también cuenta con momento angular, L. La ecuación para el momento angular se ve así:

Tenga en cuenta que el momento angular es una cantidad vectorial, lo que significa que tiene una magnitud y una dirección.

el pulgar de la mano derecha señala cuando usted envuelve sus dedos alrededor de la dirección del objeto está girando).

en el sistema MKS (metro-kilogramo-segundo).

La idea importante acerca de momento angular, tanto como con la cantidad de movimiento, es que se conserva.

los principio de conservación del momento angular establece que el momento angular se conserva si no hay pares netos están involucrados.

Este principio viene muy bien en todo tipo de problemas, como cuando dos patinadores de hielo comienzan abrazados cerca mientras gira pero luego terminan con el brazo extendido. Dada su velocidad angular inicial, puede encontrar su velocidad angular final, porque el momento angular se conserva:

Si usted puede encontrar el momento inicial de la inercia y el momento final de la inercia, ya está listo. Pero también viene casos en todo menos obvios donde el principio de conservación del momento angular ayuda a salir. Por ejemplo, los satélites no tienen que viajar en orbits- circular que pueden viajar en elipses. Y cuando lo hacen, la matemática puede conseguir mucho más complicado. Por suerte para ti, el principio de conservación del momento angular puede hacer que los problemas simples.

Decir que la NASA planea poner un satélite en una órbita circular alrededor de Plutón para los estudios, pero la situación se puso un poco de las manos y el satélite terminó con una órbita elíptica. En su punto más cercano a Plutón,

las cremalleras de satélite a lo largo de 9.000 metros por segundo.

¿A este punto? La respuesta es difícil de entender a menos que se puede topar con un ángulo aquí, y ese ángulo es el momento angular.

El momento angular se conserva porque no hay pares externos el satélite debe hacer frente a la gravedad (siempre actúa paralela al radio orbital). Debido a que el momento angular se conserva, se puede decir que

Debido a que el satélite es tan pequeño comparado con el radio de su órbita en cualquier lugar, se puede considerar el satélite una masa puntual. Por lo tanto, el momento de inercia, YO, es igual a Sr². La magnitud de la velocidad angular es igual v / r, para que pueda expresar la conservación del momento angular en función de la velocidad de este modo:

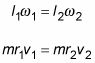
Puedes poner v₂ en un lado de la ecuación dividiendo por Sr₂:

Usted tiene su Solución ninguna fantasía matemática involucrada en absoluto, porque se puede invocar el principio de conservación del momento angular para hacer el trabajo para usted. Todo lo que necesitas hacer es conectar los números:

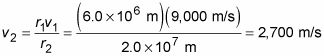
En su punto más cercano a Plutón, el satélite será gritando junto a 9.000 metros por segundo, y en su punto más lejano, se mueve a 2.700 metros por segundo. Es bastante fácil de averiguar, siempre y cuando usted tiene el principio de conservación del momento angular bajo su cinturón.