La determinación de la parte angular de una función de onda
En la física cuántica, se puede determinar la parte angular de una función de onda cuando se trabaja en los problemas que tienen un potencial central. Con problemas potenciales centrales, usted es capaz de separar la función de onda en una parte angular, que es un armónico esférico, y una parte radial (que depende de la forma del potencial).
Potenciales centrales son esféricamente simétricas potenciales, de la clase donde V (r) = V (r). En otras palabras, el potencial es independiente de la naturaleza del vector del radio vector del potencial depende sólo la magnitud del vector r (cual es r), No en el ángulo de r.
Por lo tanto, cuando se tiene un potencial central, ¿qué se puede decir de la parte angular de
La parte angular debe ser una función propia de L2, y las funciones propias de L2 son los armónicos esféricos,
(dónde l es el número cuántico total del momento angular y m es el z componente del número cuántico del momento angular). Los armónicos esféricos son iguales
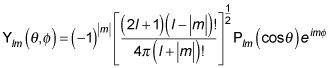
Estos son los primeros armónicos esféricos normalizados:
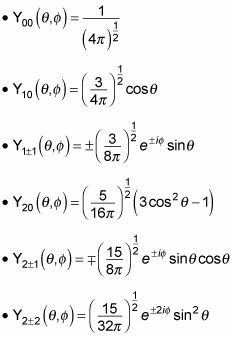
Eso es lo que la parte angular de la función de onda va a ser: un armónico esférico.
-
La aceleración angular en problemas de física -
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Aplicando la ecuación radial en el interior del pozo cuadrado -
Calcula la función de onda de un átomo de hidrógeno utilizando la schr & # ecuación 246-dinger -
Conexión de aceleración angular y el desplazamiento angular a la velocidad angular -
La determinación de la parte radial de una función de onda
Cómo angular obras de aceleración Si los puntos de velocidad de vector angular fuera del plano de rotación de una rueda, puede usar la física para determinar lo que sucede cuando los cambios de velocidad angular - cuando la rueda se acelera o ralentiza. Un cambio en la velocidad…
Cómo operadores de spin se asemejan a los operadores del momento angular Debido giro es un tipo de momento angular incorporado, operadores de spin tienen mucho en común con los operadores de momento angular orbital. A medida que su instructor de la física cuántica le dirá, hay operadores de spin análogas, S2 y Sz,…
Cómo calcular la frecuencia angular de una masa en un resorte En física, se puede aplicar la ley de Hooke, junto con el concepto de movimiento armónico simple, para encontrar la frecuencia angular de una masa en un resorte. Y debido a que se puede relacionar la frecuencia angular y la masa en la primavera,…
¿Cómo cambiar las ecuaciones de movimiento lineal para el movimiento de rotación En la física, cuando se pasa de un movimiento lineal a un movimiento de rotación, es necesario cambiar las ecuaciones que se utilizan para calcular los resultados. Aquí están los equivalentes angulares (o análogos) para las ecuaciones de…
Cómo crear estados propios del momento angular Puede crear los estados propios reales, | l, m>, de estados de momento angular en la mecánica cuántica. Cuando usted tiene los estados propios, usted también tiene los valores propios, y cuando se tiene los valores propios, puede resolver el…
Cómo determinar la dirección de la velocidad angular En la física, cuando una rueda está girando, no sólo tiene una velocidad angular, sino también una dirección. Esto es lo que el vector velocidad angular le dice:El tamaño del vector velocidad angular le indica la velocidad angular.La…
¿Cómo encontrar valores propios del momento angular Cuando usted tiene los valores propios de estados de momento angular en la mecánica cuántica, puede resolver el hamiltoniano y obtener los niveles de energía permitidos de un objeto con el momento angular. Los valores propios del momento angular…
¿Cómo encontrar conmutadores de momento angular, l En la física cuántica, usted puede encontrar conmutadores de momento angular, L. Primera examinar LX, Ly, y yoz por echar un vistazo a la forma en que commute- si conmutan (por ejemplo, si [LX, Ly] = 0), entonces se puede medir cualquier dos de…
¿Cómo encontrar las funciones propias de l2 en coordenadas esféricas Su instructor física cuántica puede pedirle que encontrar las funciones propias de la L2 en coordenadas esféricas. Para ello, se comienza con la función propia deldado que en coordenadas esféricas, la L2 operador tiene este aspecto:Eso es todo…
¿Cómo encontrar la función de onda del estado fundamental de un oscilador cuántico En la física cuántica, se encuentra la función de onda del estado fundamental de un oscilador cuántico, como la que se muestra en la figura, que toma la forma de una curva de Gauss.El estado fundamental de un oscilador armónico mecánica…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
En relación lineal y movimiento angular En la física, al igual que usted puede utilizar fórmulas para calcular la velocidad lineal, la aceleración, el desplazamiento y el movimiento, también puede utilizar fórmulas equivalentes para angular (rotación) movimiento.Usted puede pensar…