Aplicando la ecuación radial en el interior del pozo cuadrado
En la física cuántica, se puede aplicar la ecuación radial dentro de un pozo cuadrado (donde el radio es mayor que cero y menor que la). Para un cuadrado esférica pozo de potencial, esto es lo que la ecuación radial parece para la región 0 lt; r lt; la:
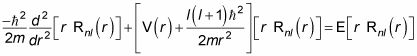
En esta región, V (r) = -V0, así que tienes
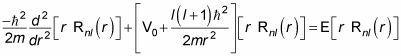
Tomando el V0 término a la derecha le da lo siguiente:
Y esto es lo divisoria por r te dio:
A continuación, multiplicando por
usted obtiene
Ahora haga el cambio de variable
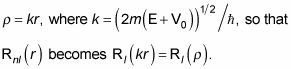
El uso de esta sustitución significa que
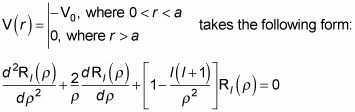
Esta es la ecuación de Bessel esférica. Esta vez,
Eso tiene sentido, porque ahora la partícula queda atrapada en la plaza así, por lo que su energía total es E + V0, no sólo E.
La solución de la ecuación anterior es una combinación de las funciones de Bessel esféricas
y las funciones esféricas Neumann
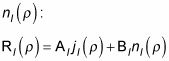
Puede aplicar la misma restricción que aquí se aplica para una partícula libre: La función de onda debe ser finita en todas partes.
las funciones de Bessel se ven así:
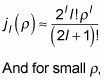
las funciones Neumann se reducen a
Así las funciones Neumann divergen para los pequeños
lo que los hace inaceptables para funciones de onda aquí. Eso significa que la parte radial de la función de onda es sólo compone de funciones de Bessel esféricas, donde Al es una constante:
La función de onda todo el interior de la plaza, así,
es un producto de radial y piezas angulares, y se ve así:
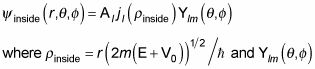
son los armónicos esféricos.
-
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Aplicando la ecuación radial fuera de la plaza, así -
La aplicación de las funciones de Bessel y Neumann esféricas para una partícula libre -
Calcula la función de onda de un átomo de hidrógeno utilizando la schr & # ecuación 246-dinger -
Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación -
Crear funciones de onda simétricas y antisimétricos para cualquier sistema de partículas n
La determinación de la parte angular de una función de onda En la física cuántica, se puede determinar la parte angular de una función de onda cuando se trabaja en los problemas que tienen un potencial central. Con problemas potenciales centrales, usted es capaz de separar la función de onda en una parte…
La determinación de la parte radial de una función de onda En la física cuántica, se puede determinar la parte radial de una función de onda cuando se trabaja en los problemas que tienen un potencial central. Con problemas potenciales centrales, usted es capaz de separar la función de onda en una parte…
Encontrar los límites de rho pequeños y grandes de una partícula libre En la física cuántica, se pueden encontrar los límites de rho pequeños y grandes de una partícula libre. De acuerdo con la ecuación de Bessel esférica, la parte radial de la función de onda para una partícula libre se ve así:Echa un…
Encontrar la ecuación de energía total para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer a encontrar la ecuación de energía total para los problemas de partículas libres tridimensionales. La energía total de la partícula libre es la suma de la energía en tres…
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
¿Cómo un aumento en r afecta la apariencia de las funciones de onda de hidrógeno En un átomo de hidrógeno, las funciones de onda cambian a medida que cambia el radio orbital, r. Entonces, ¿qué se ven las funciones de onda del hidrógeno como? Dado queSe ve como esto:Aquí están algunas otras funciones de onda de…
Cómo física cuántica convierte el impulso y la posición en probabilidades La física cuántica, a diferencia de la física clásica, es completamente determinista. Nunca se puede saber la preciso posición y el momento de una partícula en un momento dado. Usted puede dar sólo probabilidades para estas mediciones…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener las funciones de onda incidente y dispersos de partículas spinless Desde un punto de la física cuántica independiente del tiempo de vista, se puede derivar la onda incidente y funciones de onda dispersos de dos partículas no relativistas spinless. Para ello, es necesario asumir que la interacción entre las…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:La función de onda es una onda…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…