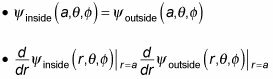Aplicando la ecuación radial fuera de la plaza, así
En la física cuántica, se puede aplicar la ecuación radial fuera de un pozo cuadrado (donde el radio es mayor que la). En la región r > la, la partícula es igual que una partícula libre, así que esto es lo que la ecuación radial se ve así:
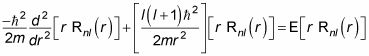
A resolver esta ecuación de la siguiente manera:
sustituyes
de manera que Rnl(r) Se convierte
El uso de esta sustitución significa que la ecuación radial toma la siguiente forma:
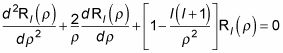
La solución es una combinación de funciones de Bessel esféricas y funciones esféricas Neumann, donde bl es una constante:
Si la energía E lt; 0, debe tener Cl = I Bl", De modo que la función de onda decae exponencialmente a grandes distancias r. Así que la solución radial fuera del pozo cuadrado tiene este aspecto, donde
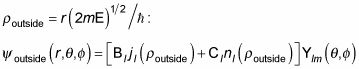
Teniendo en cuenta que la función de onda dentro del pozo cuadrado es
Así que, ¿cómo encontrar las constantes Al y Bl? Usted encontrará esas constantes a través de restricciones de continuidad: En el interior / frontera exterior, donde r = la, la función de onda y su primera derivado debe ser continua. Por lo tanto para determinar unal y Bl, usted tiene que resolver estas dos ecuaciones:
-
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
La aplicación de las funciones de Bessel y Neumann esféricas para una partícula libre -
Aplicando la ecuación radial en el interior del pozo cuadrado -
Calcula la función de onda de un átomo de hidrógeno utilizando la schr & # ecuación 246-dinger -
Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación -
La determinación de la parte radial de una función de onda
Encontrar los límites de rho pequeños y grandes de una partícula libre En la física cuántica, se pueden encontrar los límites de rho pequeños y grandes de una partícula libre. De acuerdo con la ecuación de Bessel esférica, la parte radial de la función de onda para una partícula libre se ve así:Echa un…
Encontrar la ecuación de energía total para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer a encontrar la ecuación de energía total para los problemas de partículas libres tridimensionales. La energía total de la partícula libre es la suma de la energía en tres…
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
¿Cómo un aumento en r afecta la apariencia de las funciones de onda de hidrógeno En un átomo de hidrógeno, las funciones de onda cambian a medida que cambia el radio orbital, r. Entonces, ¿qué se ven las funciones de onda del hidrógeno como? Dado queSe ve como esto:Aquí están algunas otras funciones de onda de…
Cómo agregar dependencia del tiempo y obtener una ecuación física para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer que usted agregue dependencia del tiempo y obtener una ecuación física para un problema partícula libre en tres dimensiones. Puede agregar dependencia del tiempo de la solución…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener las funciones de onda incidente y dispersos de partículas spinless Desde un punto de la física cuántica independiente del tiempo de vista, se puede derivar la onda incidente y funciones de onda dispersos de dos partículas no relativistas spinless. Para ello, es necesario asumir que la interacción entre las…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:La función de onda es una onda…
¿Cómo mantener una función de r finito cuando r tiende a infinito En la física cuántica, la hora de encontrar la solución para una ecuación radial para un átomo de hidrógeno, que necesita para mantener la función de r finito como r tiende a infinito para evitar que la solución se vuelva no físico. Usted…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…