Encontrar la ecuación de energía total para los problemas de partículas libres en tres dimensiones
En algún momento, su instructor física cuántica puede querer a encontrar la ecuación de energía total para los problemas de partículas libres tridimensionales. La energía total de la partícula libre es la suma de la energía en tres dimensiones:
E = EX + Ey + Ez
Con una partícula libre, la energía de la X componente de la función de onda es
Y esta ecuación funciona de la misma manera para el y y z componentes, así que aquí está la energía total de la partícula:
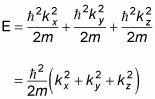
Tenga en cuenta que kX2 + ky2 + kz2 es el cuadrado de la magnitud de k - eso es,
Por lo tanto, se puede escribir la ecuación de la energía total como
Tenga en cuenta que debido a E es una constante, no importa donde se señala la partícula, todas las funciones propias de
son degenerados infinitamente como varías kX, ky, y kz.
-
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Aplicando la ecuación radial fuera de la plaza, así -
Aplicando la ecuación radial en el interior del pozo cuadrado -
La determinación de los niveles de energía de una partícula en un potencial cuadro -
Encontrar los límites de rho pequeños y grandes de una partícula libre -
Encontrar las x, y, z y ecuaciones para los problemas de partículas libres en tres dimensiones
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
Cómo física cuántica convierte el impulso y la posición en probabilidades La física cuántica, a diferencia de la física clásica, es completamente determinista. Nunca se puede saber la preciso posición y el momento de una partícula en un momento dado. Usted puede dar sólo probabilidades para estas mediciones…
Cómo agregar dependencia del tiempo y obtener una ecuación física para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer que usted agregue dependencia del tiempo y obtener una ecuación física para un problema partícula libre en tres dimensiones. Puede agregar dependencia del tiempo de la solución…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener las funciones de onda incidente y dispersos de partículas spinless Desde un punto de la física cuántica independiente del tiempo de vista, se puede derivar la onda incidente y funciones de onda dispersos de dos partículas no relativistas spinless. Para ello, es necesario asumir que la interacción entre las…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:La función de onda es una onda…
¿Cómo encontrar la energía total de un sistema de múltiples partículas El hamiltoniano representa la energía total de todas las partículas en un sistema multi-partícula. Puede describir ese sistema en términos de la física cuántica. La siguiente figura muestra un sistema de múltiples partículas donde un número…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
La física cuántica y el hamiltoniano Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…
La física cuántica para los maniquíes Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…