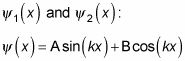¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito
Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger ecuación.
Echa un vistazo a lo infinito pozo cuadrado en la figura.
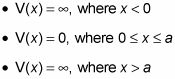
Esto es lo que la plaza también se ve así:
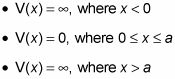
El Schr # 246-dinger ecuación tiene este aspecto en tres dimensiones:
Escribir la ecuación Schr # 246-dinger le ofrece lo siguiente:
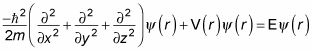
Usted está interesado en una sola dimensión - X (distancia) - en este caso, por lo que el Schr # 246-dinger ecuación parece
Debido a V (X) = 0 en el interior del pozo, la ecuación se convierte en
Y en problemas de este tipo, la ecuación se suele escribir como
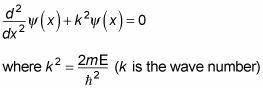
Así que ahora usted tiene una ecuación diferencial de segundo orden para resolver la función de onda de una partícula atrapada en un cuadrado infinito también.
Te dan dos soluciones independientes porque esta ecuación es una ecuación diferencial de segundo orden:
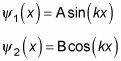
A y B son constantes que aún están por determinar.
La solución general de
es la suma de
-
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Aplicando la ecuación radial fuera de la plaza, así -
Aplicando la ecuación radial en el interior del pozo cuadrado -
Calcula la función de onda de un átomo de hidrógeno utilizando la schr & # ecuación 246-dinger -
Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación -
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:La función de onda es una onda…
Cómo cambiar la simétrica cuadrada bien en torno al origen Pozos cuadrados Infinitas, en el que las paredes van a infinito, son uno de los favoritos en los problemas de la física cuántica. En algunos casos, es posible que desee cambiar las cosas para que el pozo cuadrado es simétrica alrededor del…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
La física cuántica para los maniquíes Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…
Resolución de la función de onda pequeña ry r grande utilizando el schr & # ecuación 246-dinger Su instructor física cuántica puede pedirle que resuelva para la función de onda para una partícula inventada de la masa m en un átomo de hidrógeno. Para hacer esto, puede comenzar utilizando un Schr # 246-dinger ecuación modificada que…