Cómo obtener la ecuación 246-dinger schr & #

En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.

Werner Heisenberg desarrolló la vista matriz orientada de la física cuántica, a veces llamada la mecánica matricial. La representación de la matriz está bien para muchos problemas, pero a veces hay que ir más allá de ella, ya que estás a punto de ver.

Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de energía se llama el hamiltoniano, H, y la búsqueda de los niveles de energía de un sistema se rompe a la búsqueda de los valores propios del problema:

Aquí, E es un valor propio del operador H.

Aquí está la misma ecuación en términos de matriz:

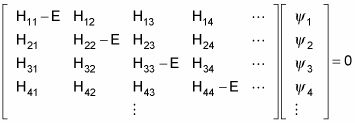
Los niveles de energía permitidos del sistema físico son los valores propios E, que satisfacen esta ecuación. Estos se pueden encontrar resolviendo el polinomio característico, que se deriva de establecer el determinante de la matriz de arriba a cero, como tal

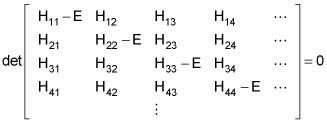
Eso está bien si usted tiene una base discreta de vectores propios - si el número de estados de energía es finita. Pero ¿y si el número de estados de energía es infinita? En ese caso, ya no se puede utilizar de forma discreta para sus operadores y sujetadores y mercados - se utiliza un continuo base.

En representación de la mecánica cuántica en una forma continua es un invento del físico Erwin Schr # 246-dinger. En la base continua, se convierten en sumas integrales. Por ejemplo, tomemos la siguiente relación, donde I es la matriz identidad:

Se convierte en la siguiente:

Y cada mer-

se puede ampliar en una base de otros mercados,

Me gusta esto:

Echa un vistazo a la posición del operador, R, en una base continua. La aplicación de este operador le da r, el vector de posición:

En esta ecuación, aplicando el operador de posición a un vector de estado devuelve los lugares, r, que una partícula puede encontrarse en. Puede ampliar cualquier cado en la base de posición así:

Y esto se convierte

Aquí hay una cosa muy importante entender:

es el ola función para el vector de estado

- es la representación de la ket en la base posición.

O en términos comunes, es sólo una función, donde la cantidad

representa la probabilidad de que la partícula se encuentre en la región d³r centrada en r.

La función de onda es la base de lo que se llama mecánica ondulatoria, en contraposición a la matriz mecánica. Lo importante es darse cuenta de que cuando se habla de representación de los sistemas físicos de la mecánica ondulatoria, no use los sujetadores y mercados de matriz básicos menos mechanics- más bien, por lo general, utiliza la función de onda - es decir, los sujetadores y los mercados en la base posición.

Por lo tanto, se pasa de hablar de

Esta función de onda es sólo una cado en la base posición. Así que en la mecánica ondulatoria,

se convierte en la siguiente:

Puedes escribir esto como el siguiente:

Pero lo que es

Es igual a

El operador hamiltoniano, H, es la energía total del sistema, cinética (p²/ 2m), Además de potencial (V (r)) Para que pueda obtener la siguiente ecuación:

Pero el operador de momento es

Por lo tanto, sustituyendo el operador impulso para p te da esto:

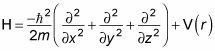
Usando el operador laplaciano, se obtiene la siguiente ecuación:

Puede volver a escribir esta ecuación como la siguiente (llamado Schr # 246-dinger ecuación):

Así que en la vista de la mecánica ondulatoria de la física cuántica, que está ahora trabajando con una ecuación diferencial en lugar de múltiples matrices de elementos. Todo esto venía de trabajar en base a la posición,

Al resolver el Schr # 246-dinger ecuación para

usted puede encontrar los estados de energía permitidos para un sistema físico, así como la probabilidad de que el sistema estará en un cierto estado de posición.

Tenga en cuenta que, además de funciones de onda en la base de posición, también puede dar una función de onda en la base impulso,

o en cualquier número de otras bases.